When you solve a triangle or find an unknown angle, the angle measure will probably be in degrees.
The gray box below lists the kinds of triangles one may "solve" -- figure out the measures of all the angles and side.

Because you, the reader, have already studied the 45-45-90 and 30-60-90 right triangles
and know the lengths of their sides and how
similar figures work, you have enough information to solve triangles listed above the white box.
Through work on this page and arcfunctions, the number of right triangles that may be solved
is greatly increased. Below the white box are listed the triangles for which more math is required to solve the
triangle, the triangles which may not be right triangles .But, now we address solving right triangles using arcfunctions.
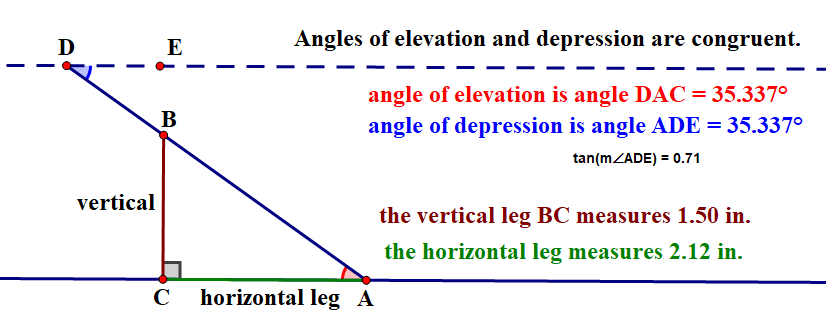
The
elevation.gps provides a movable model of the kinds of right triangle problems one might encounter.
Solve.xls provides a computation tool.
The situtation usually studied include:
- a ladder leaning against a building,
- a pole casting a shadow,
- a tree of unknown hight but with a known angle of elevation a distance from the tree
- a right triangle in which the lengths of the sides are known but the angles are not known,
- a pond the width of which is to be measured
- an air plane at a known altitude which is to hit a target a distance away from the plane
- a triangle in which some measures are known and some are not, but, all measures are needed
Q1. The world's steepest road is CA-108, along the Sonora Pass, in California. Its grade, its rise/run of 13:50,
stated as a percent is 26%. What incline, angle of elevation is this? (Source:
https://matadornetwork.com/read/steepest-highway-grades-in-the-us/)
Q2. Solve the triangle with C = 90°, a = 2.5, c= 6.
Q3. Complete from Precalc Notes, page "To Be Printed"
27. pdf of use arcfx to solve triangles con-dots.
Q4. Write and solve a word problem similar to Q1 using a "situtation usually studied" as listed above.
|
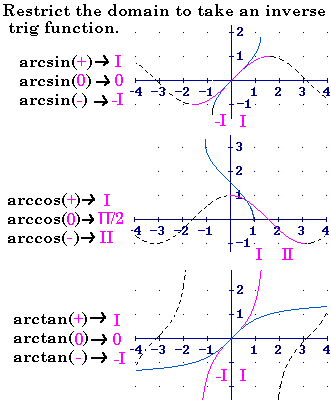



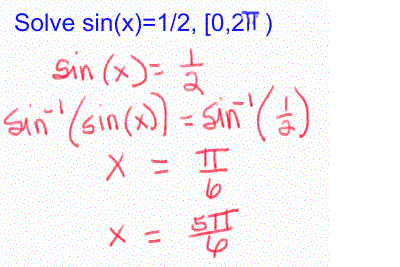
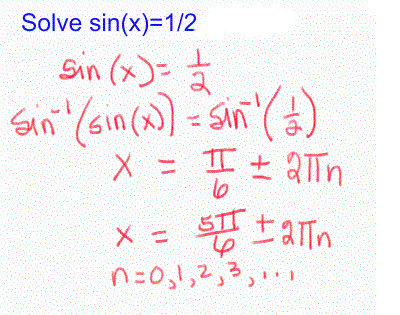



![[MC,i. Home]](http://www.mathnstuff.com/math/spoken/here/1gif/mcihome.gif)
![[Good Stuff]](http://www.mathnstuff.com/gif/goods.gif)

![[MSH! Home]](http://www.mathnstuff.com/math/spoken/here/1gif/mshhome.gif)
![[Applications]](http://www.mathnstuff.com/math/spoken/here/1gif/apply.gif)

![[Words]](http://www.mathnstuff.com/math/spoken/here/1gif/words.gif)
![[Table]](http://www.mathnstuff.com/math/spoken/here/1gif/table.gif)