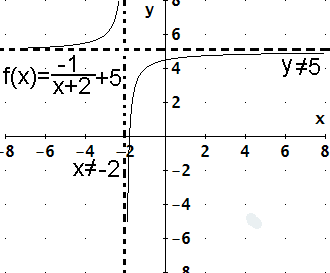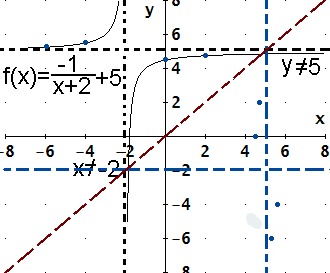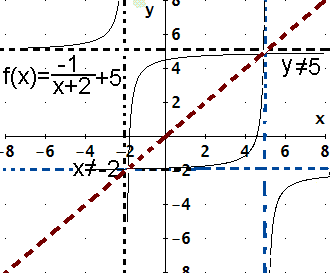|
You really do need to remember all the "inverse stuff."
|
Taking An Inverse Verbally
The inverse and the function undo each other. To understand this, consider the result of operating with the function. Consider what the function does. Read down the green box to examine what the function does. Read up the blue box to examine what the inverse does. Read left to right, green to blue to identify each inverse operation needed to achieve
the final inverse function.
|
|
|
In trig, arc functions are inverses of functions.
The arcsine, arcsin(x), may be thought of as "the angle whose sine
is x." This is not a definition, just a useful expression for an idea. The sine function
and arcsine functions exist independent of angles, but angles may be thought of as a
means of completeing compution or gaining understanding.
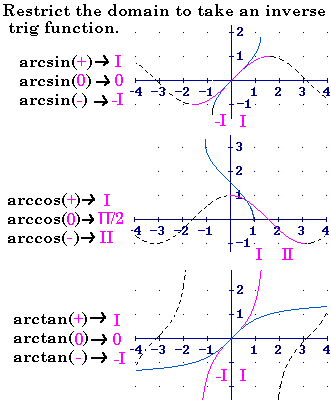
Since the trig functions are periodic they are not 1-to-1 and to have an inverse, the domain of each must be restricted. The restriction on the domain of the original function was selected so that the arcfunction returned unique values for each domain value and provided for negatives and positives. |
|
 | ![[MC,i. Home]](http://www.mathnstuff.com/math/spoken/here/1gif/mcihome.gif)
![[Table]](http://www.mathnstuff.com/math/spoken/here/1gif/table.gif)
![[Words]](http://www.mathnstuff.com/math/spoken/here/1gif/words.gif)

![[this semester's schedule w/links]](http://www.mathnstuff.com/gif/semestr.gif)
![[Good Stuff -- free & valuable resources]](http://www.mathnstuff.com/gif/goods.gif)

© 2009, Agnes Azzolino www.mathnstuff.com/math/spoken/here/2class/300/invfn.htm |

 .
. 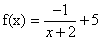
 .
. 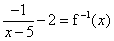
 (x - 6) + 2
(x - 6) + 2 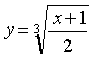
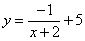
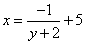
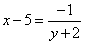
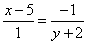
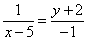
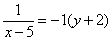
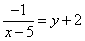
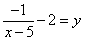
 y is not -2
y is not -2