 "Why = a(x - h)² + k?" -- EVERYTHING YOU EVER WANTED TO KNOW ABOUT A QUADRATIC BUT WERE AFRAID TO ASK
"Why = a(x - h)² + k?" -- EVERYTHING YOU EVER WANTED TO KNOW ABOUT A QUADRATIC BUT WERE AFRAID TO ASK
 "Why = a(x - h)² + k?" -- EVERYTHING YOU EVER WANTED TO KNOW ABOUT A QUADRATIC BUT WERE AFRAID TO ASK
"Why = a(x - h)² + k?" -- EVERYTHING YOU EVER WANTED TO KNOW ABOUT A QUADRATIC BUT WERE AFRAID TO ASK |
The Quadratic, y = ax2 + bx + c
|
| Quadratic | ||
| Quadratic? | Quadratic: x2, or 2x2 or -3x2 or ax2. | 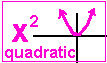 |
| Quadratic: | NOT constant (2, -3, a). |  |
| Quadratic: | NOT linear (2x or -3x or ax). |
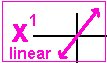 |
| Quadratic: | NOT cubic (2x3 or -3x3 or ax3). | 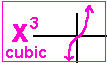 |
| Quadratic: | NOT quartic (-3x4), or higher. | 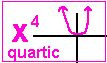 |
Quadratics are polynomials where the highest degree of the variable is 2. Quadratics are polynomials like ax2 + bx + c or a(x - h)2 + k or 2x2 -3x + 5 or 4x2 - 1 or -3x2 + 2x -6.
| ||
Uses of Quadratics
|
| THE Quadratic Equation VS. A Quadratic Equation The equation ax2 + bx + c = 0 is the
quadratic equation and its solution is
The equation y = ax2 + bx + c is a quadratic equation because its highest degree is 2. It's an equation where a, the coefficient of the quadratic or x2 term, does not equal zero. If a were 0, there would be no quadratic term. It's an equation or statement in which y is expressed in terms of a, b, c, and x. Because it's a quadratic, the graph of the curve is a parabola, a quadratic function. Quadratic functions are the second simplest of the polynomial functions.
In general polynomials look like y = anxn + an-1xn-1 + an-2xn-2 + ... +a2x2 + a1x1 + a0x0. These equations are quadratic: y = ax2 + bx + c or y = a(x - h)2 + k. |
Related Pages & Resources
|

![[MC,i. Home]](http://www.mathnstuff.com/math/spoken/here/1gif/mcihome.gif)
![[Words]](http://www.mathnstuff.com/math/spoken/here/1gif/words.gif)

![[this semester's schedule w/links]](http://www.mathnstuff.com/gif/semestr.gif)
![[Good Stuff -- free & valuable resources]](http://www.mathnstuff.com/gif/goods.gif)
|
www.mathnstuff.com/math/spoken/here/2class/320/c32pg00.htm |