

| "Why = a(x - h)² + k?" -- EVERYTHING ... ABOUT A QUADRATIC ... |
| The Best Way to Solve A Quadratic |
| The best way to solve any equation is the way that takes least effort. An equation which is easy to factor takes the least effort because it may, with practice, be solved mentally. These easy to factor equations turn up even in algebra II and calculus. So, TRY FACTORING FIRST. Occasionally a quadratic is graphed and the x-intercepts, the zeros, the solutions, may be read directly from the graph. If the graph is not clear and of the readable kind (see below) it is best not to use this method. LOOK FOR EASY TO READ ZEROS IN A GRAPH. Graphing calculator are great and for messy equations give either exact or approximate answers. See Solving Equations by Calculator. BE SURE TO LOOK FOR 2 ROOTS! The quadratic formula is always dependable and sometimes messy. Check it out. EVEN WHEN FACTORING DOESN'T WORK, THIS METHOD WILL WORK. AS A LAST RESORT, use completing the square to solve a quadratic. |
 |
| Solve A Quadratic By Graphing | |
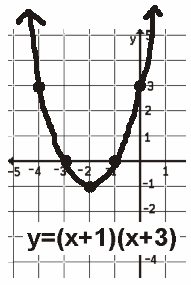
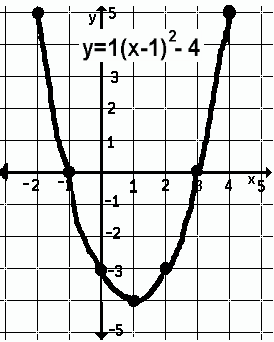
| Suppose you were good at solving equations by factoring and were told to
Solving the above equations given the graphs
Solving the equations
Solving the equations
The x-intercept is the solution. Find the x-value(s) at which the quadratic crosses the x-axis and you have found the solution(s). To solve a quadratic equation graphically, produce the graph, find the x-values at which the graph crosses the x-axis. IF THIS IS NOT POSSIBLE, CHOOSE ANOTHER METHOD. | 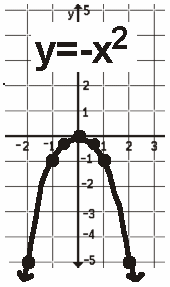
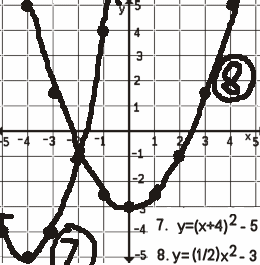
|
| Solve Quadratic By Calculator | |
For instructions on how to use the algebraic solver or polynomial solver on a calculator see Solve with a Calculator. On that page, the focus is on basic use of the machine, such as in solving linear equations. | |
|
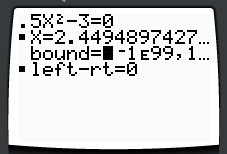
Usually parabolas and quadratics and using a calculator to find more than 1 solution is covered in algebra II. Below are calculator screens showing the two decimal approximation solutions to the equation. By changing the SEED value which starts the calculator working on solving for x, different roots may be found. | 
 |
|
The basic instruction say:
The advanced instruction say:
| |
Solve Using the CALCULATE Functions 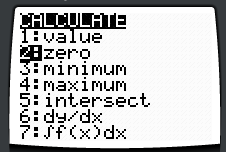 1st: Enter the function in the [y=] menu. 2nd: Enter the [CALC] menu, above [TABLE]. 3rd: Press 2:zero to start the prompts which you must answer. 4th: Answering the prompts, enter a Left Boundary and a Right Boundary about a root. 5th: Answering the prompt, select a Guess or SEED value which begins the computation to determine the root. 6th: Read the x-value, the zero. 7th: Repeat the process as needed to find desired roots. | |
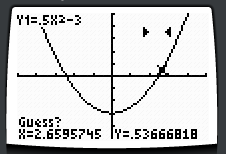 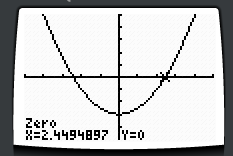
| |
|
Quadratic Equation, Formula, & The Discriminant
Briefly ... Each of the constants a, b, and c in the quadratic equation 0 = ax² + bx + c, plays a role in the number and kind of roots, assuming a is not 0. The expression b² - 4ac, the discriminant, uses the constants to determine the number and kind of roots.
For a thorough exposition of the quadratic and the discriminant, see The Quadratic Equation, Formula, & Discriminant. Briefly ... |
Solve By Completing the Square
| ||||
|
Solving a quadratic by completing the square is not something one does for fun. It was used to create the quadratic formula. It is used to solve quadratics which have variables rather than constants as coefficients though the formula is quicker. It is used as an exercise in algebra II classes.
A few algebra I reminders are needed before completing the square. To add/subtract fractions, you need a common denominator. To divide fractions, you flip the 2nd fraction and multiply straight across.
Remember: (x + y)² = x² + 2xy + y² Remember: (x + b)² = x² + 2bx + b² Remember: x² + 2bx + b² = (x + b)² If: x² +bx + _________
= (x + __)² then
If: x² +(b/a)x + _________
= (x + __)² then
Take half the coefficient of the linear term and square it. This is called completing the square. Solve ax² +bx + c = 0 by completing the square:1st: Keep terms with variables on one side and constants on the other. ax² + bx = - c 2nd: Factor the a out on the left side of the equation. ax² + bx = - c a(x² + (b/a)x) = - c COMPLETE THE SQUARE. 3rd: Work on two lines of the equation at the same time. ax² + bx = - c a(x² + (b/a)x) = - c a(x² + (b/a)x + ________) = ________ - c a(x + _____)² = ________ - c 4th: Work on three terms at the same time. Take half the coefficient of the linear term, square it, adjust each side of the equation as needed. ax² + bx = - c a(x² + (b/a)x) = - c a(x² + (b/a)x + b²/(4a²)) = a[b²/(4a²)] - c. a(x + b/(2a))² = b²/(4a) - c
5th: Complete the addition on the right side of the equation. ax² + bx = - c a(x² + (b/a)x) = - c a(x² + (b/a)x + b²/(4a²)) = a[b²/(4a²)] - c a(x + b/(2a))² = b²/(4a) - c a(x + b/(2a))² = b²/(4a) - c a(x + b/(2a))² = [b² - 4ac]/(4a) 6th: Divide both sides by a to eliminate the factor of a on the left side.
ax² + bx = - c a(x² + (b/a)x) = - c a(x² + (b/a)x + b²/(4a²)) = a[b²/(4a²)] - c a(x + b/(2a))² = b²/(4a) - c a(x + b/(2a))² = b²/(4a) - c a(x + b/(2a))² = [b² - 4ac]/(4a) a(x + b/(2a))² /a = ([b² - 4ac]/(4a)) /a (x + b/(2a))² = [b² - 4ac]/(4a²) 7th: Take the square root of both sides and simplify. ax² + bx = - c a(x² + (b/a)x) = - c a(x² + (b/a)x + b²/(4a²)) = a[b²/(4a²)] - c a(x + b/(2a))² = b²/(4a) - c a(x + b/(2a))² = b²/(4a) - c a(x + b/(2a))² = [b² - 4ac]/(4a) a(x + b/(2a))² /a = ([b² - 4ac]/(4a)) /a (x + b/(2a))² = [b² - 4ac]/(4a²)  [(x + b/(2a))²] = ± [(x + b/(2a))²] = ±
 {[b² - 4ac]/(4a²)} {[b² - 4ac]/(4a²)}
x + b/(2a) = ±  [b² - 4ac]/(2a) [b² - 4ac]/(2a) 8th: Subtract b/(2a) from both sides to solve for x. ax² + bx = - c a(x² + (b/a)x) = - c a(x² + (b/a)x + b²/(4a²)) = a[b²/(4a²)] - c a(x + b/(2a))² = b²/(4a) - c a(x + b/(2a))² = b²/(4a) - c a(x + b/(2a))² = [b² - 4ac]/(4a) a(x + b/(2a))² /a = ([b² - 4ac]/(4a)) /a (x + b/(2a))² = [b² - 4ac]/(4a²)  [(x + b/(2a))²] = ± [(x + b/(2a))²] = ±
 {[b² - 4ac]/(4a²)} {[b² - 4ac]/(4a²)}
x + b/(2a) = ±  [b² - 4ac]/(2a) [b² - 4ac]/(2a)
x = - b/(2a) ±  [b² - 4ac]/(2a) [b² - 4ac]/(2a) 9th: Add the fractions on the right side and rewrite as two solutions if desired. ax² + bx = - c a(x² + (b/a)x) = - c a(x² + (b/a)x + b²/(4a²)) = a[b²/(4a²)] - c a(x + b/(2a))² = b²/(4a) - c a(x + b/(2a))² = b²/(4a) - c a(x + b/(2a))² = [b² - 4ac]/(4a) a(x + b/(2a))² /a = ([b² - 4ac]/(4a)) /a (x + b/(2a))² = [b² - 4ac]/(4a²)  [(x + b/(2a))²] = ± [(x + b/(2a))²] = ±
 {[b² - 4ac]/(4a²)} {[b² - 4ac]/(4a²)}
x + b/(2a) = ±  [b² - 4ac]/(2a) [b² - 4ac]/(2a)
x = - b/(2a) ±  [b² - 4ac]/(2a) [b² - 4ac]/(2a)
x = |

![[MC,i. Home]](http://www.mathnstuff.com/math/spoken/here/1gif/mcihome.gif)
![[Table]](http://www.mathnstuff.com/math/spoken/here/1gif/table.gif)
![[Words]](http://www.mathnstuff.com/math/spoken/here/1gif/words.gif)

![[this semester's schedule w/links]](http://www.mathnstuff.com/gif/semestr.gif)
![[Good Stuff -- free & valuable resources]](http://www.mathnstuff.com/gif/goods.gif)
|
www.mathnstuff.com/math/spoken/here/2class/320/qsolve.htm |