If ax² + bx + c = 0 then x = .

    The first equation is called the general form of a quadratic equation. The second equation is called the Quadratic Formula because it states the solution -- provides a formula for computing the simplified answer(s) by using the values of the first equation.

    Restated: If an equation can be rearranged to look like ax² + bx + c = 0 then at most two answers answers may be found by using these formulas:

x = 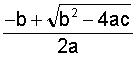and x = .

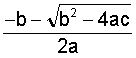    This page can be used to:

• Solve, with a real decimal approximation, an equation in
  ax² + bx + c = 0 form, or
• Go step by step through the solution.

Solve the equation x² + 3x = - 2x - 6 or others like it.

 

1st: Move all the terms to one side of the equation.

This would mean that there is a 0 on the other side of the equation.

x² + 3x = - 2x - 6

x² + 5x = - 6

x² + 5x + 6 = 0

 

2nd: Arrange the equation in descending order.

Have the terms listed so the the highest degree is first, the next highest degree is second...

In other words, state the quadratic term first, the linear term second, the constant term last.

It should look like:     ax² + bx + c = 0

3rd: Record values here for a, b, and c.

Remember, the sign is included in the value of each constant.

x² + x + = 0

 

4th: Replace each variables with its value in the expression

   

      b² - 4ac

()² - 4 () ()

 

5th: ,   b² - 4ac

to determine the number and kind of roots.

The discriminant is .

discriminant is	number of roots	kind of roots
zero, b² - 4ac = 0	1	real (double)
positive, b² - 4ac > 0	2	real
negative, b² - 4ac < 0	2	complex

 

5th: Replace variables as required.

becomes

- ± ()         2

6th: Factor and reduce if possible.

 

7th: If the discriminant is negative, restate in terms of  i , (-1).

1st: Arrange your equation so it looks like:

ax² + bx + c = 0

2nd: Input the values:

x² + x + = 0

 

      If the discriminant is negative, the roots are complex, and this page can not display the complex number. The output will be "NaN."

3rd: Press for the root

,

 

4rd: Press for the root

,