Angle Measure

      A number is a thought. I really do not know, but, it is likely numbers were first used for counting. In early societies and until "recently" is primitive societies, numbers didn't go "very high." There were words for 1, 2, and perhaps a phrase meaning "more than 2."

      One may have also needed to communicate a number to another human.  Those who needed numbers had agreed upon meanings for the numbers. In early societies, communication of a number was likely done by pointing to a body part and this method was used, at least until "recently" in primitave societies.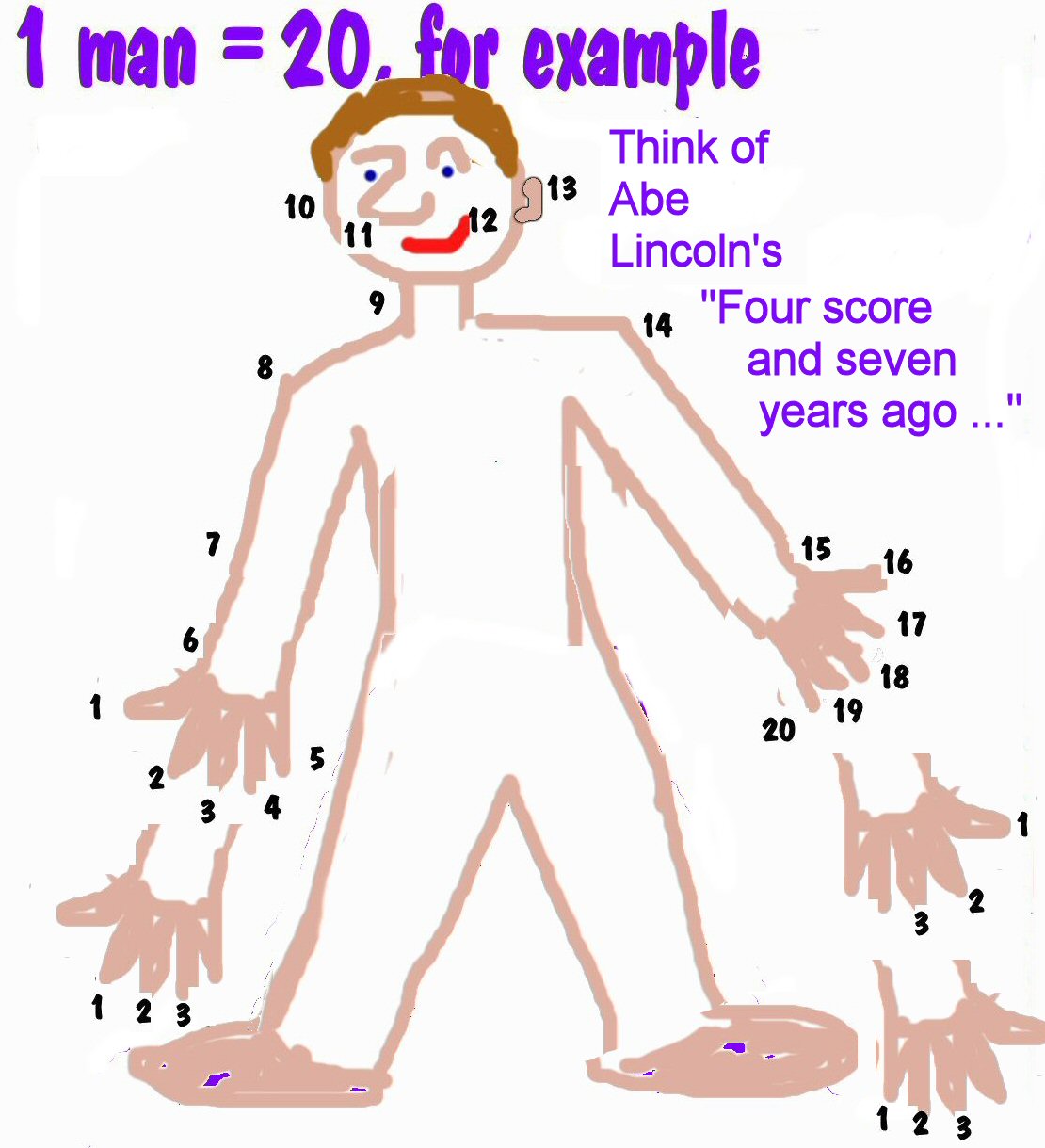

      As body pointing to communicate a number varied from human group to human group, the pointing required also varied. On the figure, notice different ways of counting 1, 2, and 3.

      As societies AND TECHNOLOGIES evolved, mathematics evolved. number and numeration symbols, and methods of computation vary and change. Arabraic/Indian 10-digit numeral were, I believe, not very useful until paper became cheap enough for writing. Papyrus and velum were, I think, too expensive for computation purposes. Paper was the new technology.  See the excellent books on number systems and counting:   Claudia Zaslavsky's "Africa Counts," Denise Schmandt-Besserat's "History of Counting," and Karl Menninger's "Number Words and Symbols" .

    Over time and in different locations, angle measure also varied and changed.

      Ancient Egyptians who built the pyramids, used an additive numeration system, used unit fractions for numbers which were parts of a whole, and added and subtracted and multiplied and divides with a kind of counting board. The multiplications and divisions were completed with binary notation. Their mathematics BUILT THE PYRAMIDS! They were sophisticated mathematicians. Yes, the measured in cubits and palms, and fingers, but that worked well enough to build the pyramids.

    If you're thinking, "Yah, yah, I know all that" you probably recognize the Eye of Horus. Do you know the story behind the image? Do you REALLY know the story? Click on the image to see.

    I can picture an ancient Egyptian pointing to communicate a fraction.

    For angles, they did not use degrees or even "say" angle. They went directly to a computational definition. For an "angle" measure, they used the ratio of the vertical length to the horizontal length, what we would today call the slope or tangent. They did just basic stuff, right? No way. What we call the sine of an angle, they called a half chord. (See the length of segment BP on sheet 10 of limit.gsp).   It is the sine of red angle theta.  No angle meaure symbol needed, just the mathematics of the situation. Their thought was much more physical and geometric than we daily use now.

    The Sumerians used base 60, sexagesimal system based on 60 rather than the centesimal system based on units of 10. They divided both day and night into twelve hour intervals. From them we get angles measured in degrees and minutes and seconds and 360° in a full circle.

    Where did 360° come from?

    Most math historians point to this choice of 60 for its very desirable factorability and its very desirable divisability by 2, 3, 4, 5, 6, 10, 12, 15, 20, and 30.  Humans have been thinking primes and divisability since way before these ideas were documented in words.   The Ishango Bone may be 20,000 years old.

    Here consider the geometric desirability of a base of 60.   Check out the video and Sketchpad.

    Their astronomy was excellent.   Their angles measured by degrees was a really big contribution to human kind.

    The Ancient Greeks and Romans both used base 10. They wrote with "Roman numerals" and computed on a board using stones, called calculi, from which we get the word calculus. I think the Ancient Egyptians also used this kind of table or board, but, I do not know for sure.

    See abax (sand table) & reckoning board, and, one really doesn't need to know any of the above with respect to angle measure.

The Greeks and Romans gave us:
• the word angle, from the Latin word angulus, meaning "corner"
• Euclid's Elements which formalized geometry
• Latin (from the Romans) as the language through which the scholarly -- even from different countries -- communicated.
• the letters of the Greek alphabet: α (alpha), β (beta), ..., θ (theta), used to label angles and their measures, and π (pi)

    In a circle (as elsewhere), pi is the ratio of a circle's circumference to its diameter. Think "around compaired to across."

    In a polygon, "around compaired to across" would be the ratio of the perimeter to the diagonal. The images linked below, use regular polygons.

    Examine
(1) the square   hexagon   octagon   dodecagon, then
(2) Approximate Pi Using the Perimeter of a Dodecagon, then
(3) Squeezing Pi Between Inscribed and Circumscribed Hexagons, then
(4) the shape of a 96-sided polygon, as used by Archimedes to approximate pi.

    For a really good history piece, read Patricia Rothman's " The Man Who Invented Pi" published in "History Today," Volume 59 Issue 7 July 2009

    She quotes in medieval Latin then English, "quantitas in quam cum multiflicetur diameter, proveniet circumferencia (the quantity which, when the diameter is multiplied by it, yields the circumference)."   What's that? π

    She also states, "Mathematicians began using the Greek letter π in the 1700s. Introduced by William Jones in 1706, use of the symbol was popularized by Leonhard Euler, who adopted it in 1737."

    Angles were in the minds of humans long before the Ancient Egyptians found trig functions of angles, even before the Greeks/Romans introduced the word angle. The Sumerians/Babylonians introduced the 360 divisions of the central angle of a circle, the degree. The Welch, in William Jones, used the symbol π for the "around compaired to across" ratio of a circle. But the symbol wasn't really useful until the German Euler popularized it so that everyone in the math community could communicate using the symbol that, the symbol became valuable for angle measure. Before the symbol became popular, the phrase, "quantitas in quam cum multiflicetur diameter, proveniet circumferencia" was used. It is known that π is irrational and transendental and the human race could now take the next step in the development of angle measure.

    Again, once a symbol was popular enough so that all could communicate using the symbol, the word and the symbol π become useful and powerful. The math always existed, now humans could conviently speak of it.

    A radian is the angle measure of today. Yes, there are also units called gradians and steridians. Yes, degrees are still used and very valuable. Radians facilitate examining trig functions, functions once only considered with respect to a circle.

    The list below comes from radian at https://en.wikipedia.org.

• "The idea of measuring angles by the length of the arc was already in use by other mathematicians. For example, al-Kashi (c. 1400) "
• "Roger Cotes in 1714.[8][9] He described the radian in everything but name"
• Azzolino's "cleanest" definition of radian is found here, on Wikipedia,
  The "International Bureau of Weights and Measures 2019, p. 151:
  "One radian corresponds to the angle for which s = r"
• It is a System International, SI, metric unit.
• "The radian is defined in the SI as being a dimensionless unit with 1 rad = 1."

    The remaining links offer mathnstuff.com material used to teach graphing, angles, radians.

    Most students know one must use radians to graph trig functions. This image shows why a radian marked x-axis is desirable. See 260radians.marked.jpg, a 9x9 plane with radians marked on the x-axis, and a bunch of other graph papers, and here the best is saved for last.

Here are:
• a pdf file of this page except for the last link: angle.measure.pdf
• a video of all but the last link of this page: angle.measure.mp4
• a video of all the last link: radianSector.mp4
• the Sketchpad used to teach radians and sectors: radianSector.gsp

    The reader is welcome to download any thing here. Enjoy.