| This page began as a simple list of the 21st-century versions of ancient computing devises listed in chronological order. The goal was to use the digital manipulative, to examine the ancient devise. It has become a bit of a research project, a report, a connect-the-dots summary connecting one developement to another both mathematically and technically. So, the simple list was created but so was a "history" or "story." This is not the "official" version of math history, but rather the "Azzolino" version based on internet research in computing devises, money, barley & wheat, and linguistics. Since this is now a history project as well as a math project, proof takes a slightly different form. It is left for the reader to determine the "truth." The works cited are listed below and the "Azzolino version" is clearly stated. Enjoy.
|
Fingers & Talley Sticks
Tokens & Coins
Shekel to Stater, Creation of Money, Credit before Coin
Writing Numerals
A Bit About Bases
Abaxes (Sand Table), Reckoning Boards, Banks
Abacuses
Napier's Bones
Slide Rules
Manipulatives & Digital Manipulatives
End Notes
|
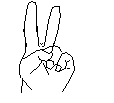 Face it, humans still use their fingers for counting and for communicating a count nonverbally from human to human.
Yes, fingers are occassionally used for multiplication. See the 9 Times Table on Your Fingers and the digital manipulative for that. Here we consider the computational devises of the human race, in the early stages of man and of counting devises. Some experts consider fingers the original computation devise and talley sticks the next oldest devise. Other experts do not consider fingers a counting devise. You decide the truth. Perhaps a talley or record of a number does not seem significant. Jeremy Norman list these two as significant each having to do with measurement of time. [1]
David Birch list these two as significant. [2]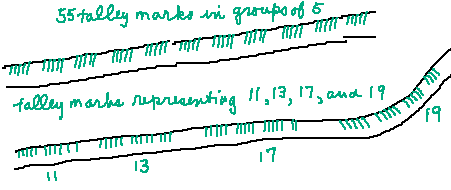 
The second is astounding! Someone noted and recorded prime numbers even before the words or symbols for numbers were recorded!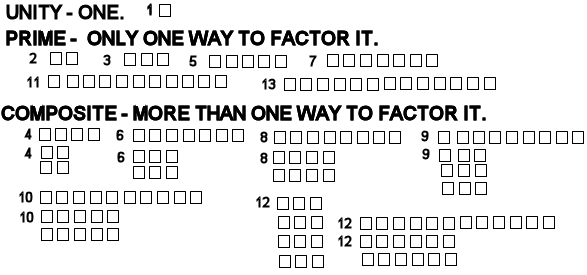 
In this "Azzolino version" of math history, this is evidence that at least 1 individual wrote about the nature of number. Yes, it is only written in talley marks, but, prime is a major concept, and primes are in evidence here. In the "Azzolino version," an individual who noted the prime vs composite nature of one thing would have tested that nature on other things. So, rather than the prime or compositeness of the thing it would be the prime and compositeness of the number since that is the shared characteristic. Back to the task at hand. Talley sticks are a valuable way of recording. It is easy with tally marks to "add it to itself" (double), a task early Egytpians used in an excellent way. Their strengths, permanent representation and the ability to add more talley marks, are also computational weaknesses. What is written can not be subtracted or changed. |
|
Take a brief trip.
Tokens and coins can represent, be added to, be subtracted from, and be changed. Their strength is their temporary permanence. They permit concrete computation. Because multiplication may be thought of as repeated addition and division may be considered repeated subtraction, these operations are also possible using concrete, manipulative, manipulation.
Think "little clay objects," statues or pictures in clay, tokens, 8 thousand to 12 thousands years old. Let a model or shapes stand in for a bushel of grain, an animal, a quantity of liquid. Collect a number of these in a pile or bag or basket and let the collection represent "your stuff." Let two or three tokens stand for two or three of the item each represents. Let larger tokens or those marked more intrecately stand for larger quantities or more intrecate items. If you wish to digitally touch or move or hold them in your hands, open the spread sheet. Between 10,000 and 6,000 B.C., in Turkey, Palestine, Syria, and Iran, says Denise Schmandt-Besserat, humans did just that -- use models or tokens to represent things thereby creating a concrete reckoning and counting system, the precurser to written symbols and recording.[4] |
 Think Sumer, Sumeria, say 3200 years ago. Start with some wheat, say a "bushel of wheat," a shekel. ["She" means "wheat" and "kel" means a unit equal to about a bushel.] [5] One thing you might do is thank Ishtar, the Goddess of Fertiltiy in Sumeria, or Isis in Egypt, and ask for a good harvest next season. To do this you went to her temple and paid for sacred prostitution. This is a really sacred act. The men were by proxy performing the act with the Goddess Ishtar. The women at the temple were performing a sacred duty just as the Vestil Virgins would perform sacred acts in the Roman era. 
Bernard Lietar describes the first coin, the shekel and says it was created to pay for this sacred service [5]. It sure beat having to carry a bushel of wheat with you. All you would need to do was bring the coin. The coin itself had a picture of Ishtar on one side and wheat on the other [5]. Wheat is the symbol of fertility and may be seen in the modern era on US "wheat pennies" of the 1950s. 
The Ishtar on the picture of the fake shekel shows just a head. Often she is seen as a winged holding snakes in her hands and standing with a star at her head. "Ishtar" means "star." Today the shekel refers to the Isreal coin. The shekel, and the bank (or temple) in which the wheat was stored in exchange for the shekel, might be seen as outgrowths of the token. This would mean the tokens described above were true "advancements" of society and not just of mathematics. There is another feature of the clay tokens and coins which is important for the next development in computing devises - bases. Suppose you had a really good harvest.
Rather than give you 30 tokens for 30 bushels of wheat, you might receive one copper bushels to represent the bushels of wheat.
James W. Bell reports that Sumerians used a silver standard. [6]
In terms of tokens, or coins, this would produce a system in which a token, or coin, of one kind would be worth a number of tokens of another kind. One might make gold worth the most "stuff," silver worth fewer of that same "stuff," copper worth fewer yet of that same "stuff," which was recorded as a simple clay token, representing the actual thing. If you wish to experiment with this token swapping, open the spread sheet and go to the "units" worksheet.
We know the Sumerians used 60 as the base for time and angle measure. We still use the same today. Our degrees and minutes and seconds are base 60.
Reid Goldsborough ignores the temple-issued shekel and considers the first minted coins to be staters [7]. Made of an alloy of silver and gold, called electrum, the stater from Lydia, now Turkey, also came in parts of a stater. The stater, "weighter" or "that which balances the scales," and the larger fractional parts -- the third stater or "trite," sixth stater or "hekte," and twelfth stater or "hemihekte" -- have a Lydian lion with a star at its head over a bull, or parts of this picture.
Smaller fractional parts -- the twenty-fourth stater, forty-eight stater, and ninety-sixth stater have a lion's paw instead. He dates these coins to 610 BCE and notes that coins in China (600 BCE), Greece (550 BCE), Athens, Corinth, and Rome (509 BCE) followed. [7] Roman coins used base 10 rather than base 6. The US Dollar and the Euro are also base 10 and exemplify value differences through size and intracacy.
Experiment with digital manipulative coins using basic computer commands.
With these digital manipulatives and good old select/copy/paste commands you can:
Coins are not, however, positional. They incorporate bases which are also used by a positional system. They may be positioned and, I believe, this also helped lead to the creation of a positional number system, but, they are not positional. Reckoning boards and banks are. Before work with boards, banks, and the abacus, work is needed on numerals and bases. In Summary
|
|
As O'Connor and Robertson point out, the earliest Greek numerals did not represent numbers but numbers of things or amounts of money [8]. This is consistent the perspective that tokens for stuff set the stage for written records. O'Connor and Robertson also discuss the development of variety of Greek numerals matching a variety of Greek city states, the development of numerals from the spoken name to the first letter of the spoken work to a written symbol, and the use of Greek letters in an additive system to represent numbers.
Writing numerals is an important commptational tool but only briefly addressed on this page. Listed below are resources one might find useful when studying written and symbolic notation. It is important to know the terms additive, multiplicative, and positional systems.
|
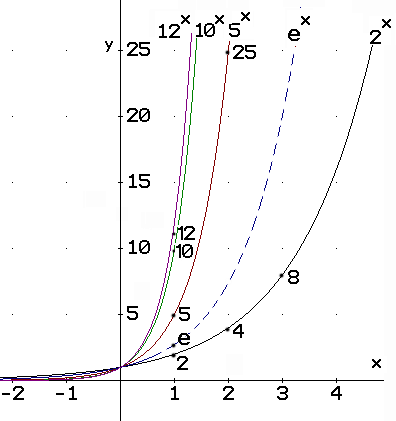As described above, number systems and their bases may have appeared to have simply
evolved. But, how and why?Considerations include:
The Sumarians used base 60, not shown in the above graph. They were able to express large numbers like 60 (the number of seconds in a minute and the number of minutes in an hour, and the number of minutes in a degree). They could easily express 3600, the number of seconds in an hour, and 360, a tenth of that, for the number of degrees in a circle. We still use base 60 in expressing angle measure and time. The number 60 divides nicely by 2, 3, 4, 5, 6, 10, 12, 15, 20, and 30 making it idea for parts of the base number.
The Egyptians used unit fractions and a base 10 additive system for representation, but a superlative base-2 technique for multiplication and division. The Romans ended up with base 10 but also used biquinary for their abacus and some sand tables or reckoning boards. At present, base 2 and base 8, and base 16 are often used for computers, base 16 is used for color and graphics, base 10 is used for daily, science, and commercial computation, base e is used in science and mathematics. Reflections & Resources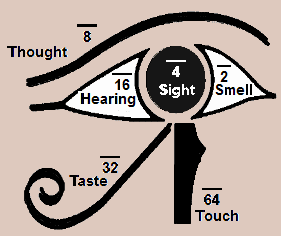
An analysis of bases as presented above is not included in most US math curriculum until freshman liberal arts math courses. It is presented here as background for a teacher, elementry school on up.
|
|
"Do not disturb my circles," said Archimedes, to the Roman soldier attacking Syracuse [10]. His sand table was not big enough to do the work he wished so he drew his math in the beach sand as the city was under attack. It cost him his life. So goes the legend. He is well known for this moment of death but even better known for his estimation of pi, formulas for the surface and volume of a sphere and cylinder, and his naked run down the street upon his discovery of buoyancy. He is remember for shouted "Eureka, eureka (I have found it)!" as he ran down the street. Archimedes invented the Archimedes screw, levers, the burning mirror, and pulleys, but he legacy includes his dedication to the circles in the sand. Though Archimedes' work was to large for a sand table, others used them. An abax (sand table) is a flat board or surface dusted with sand so a figure might be traced on the surface. Stones (calculi), were added for counting and then columns for place valued arithmetic. In general an abax has groves in which the stones slide but an abacus as rods on which the beads slide. In general, an abax is a piece of furniture and an abacus is a hand-held portable devise. A sand table with reckoning board permitted on to compute both graphically and "digitally." They were used from Greece times through the Middle Ages (by then called banco or bank or bench), but, eventually sand wasn't needed and paper could be placed on the flat board and used in conjunction or independent of the computational machine. When a merchant or banker or one seated at the counting bench or board was unable to pay bills, the bank or bench was broken, rupt, and the individual declared bankrupt [11]. Features of board and tables include:
Different versions of the reckoning table or bank are provided in digital manipulative form.
|
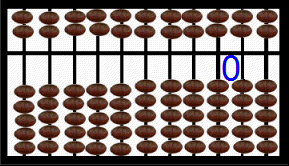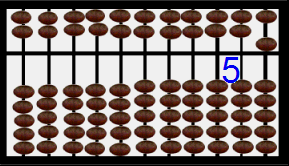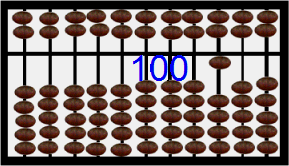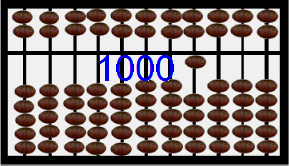
By now the Chinese saunpan at the right is displaying 1000 in blue digits and in the placement of the beads. Hit refresh on your browser or perhaps F5 on your keyboard and watch the beads cycle below (with earth beads) and above (with heaven beads) from 1 to 5 to 10 to 50 to 500 to 1000 [12]. Notice that the display area is the stationary bar that seperates the heaven beads worth 5 and the earth beads worth 1 each. This abacus is biquinary. Others are decimal. Examine those shortly. Read Totton Heffelfinger & Gary Flom's work to really learn how to use an abacus for speed of computation [12]. Read Luis Fernandes' work to learn the history of the abacus [13]. Features of an abacus include the number of beads in the heaven and earth and the base used.
Examine differenct versions of the abacus in digital manipulative form.
|
|
Napier's Bones are so cool. They were used to multiply, divide, take a square root.
|
|
Instead of using tokens or things to represent numbers, slides use lengths to represent numbers.
This slide-to-the-sum technique works well with fractions as well as whole, signed, and decimal numbers, but, the counting boards used from ancient Egyptian times through the Middle Ages work better. The abacus even better, but, addition and subtraction are the easy operations. Multiplication, division, raising to powers and taking roots are more complicated and time consuming. John Napier, of Napier's Bones fame, found a way to multiply, divide, raise to a power, take a root, using addition and subtraction. The year -- 1614 [15].
A log is an exponent. When you multiply numbers, you add the exponents. When you multiply numbers, you add the logs. Napier added logs to mupliply. Edmund Gunter [15] used scales to make the addition of logs easier. On the Gunter scale, the number on the scale is the arguement of the log and the length marked is the log of that arguement.
It was William Oughtred's idea to pair two Gunter scales and slid to to perform the addition / subtraction of the logs maked on the scale.
| |||||||||||||||||
|
|
![[master list of all MSH! dictionary words]](http://www.mathnstuff.com/math/spoken/here/1gif/words.gif)
![[Good Stuff -- free & valuable resources]](http://www.mathnstuff.com/gif/goods.gif)
![[MC,i. Home, site home page]](http://www.mathnstuff.com/math/spoken/here/1gif/mcihome.gif)
www.mathnstuff.com/papers/amtnj09.htm © 2010, 2023, A. Azzolino |
[3]
