Facts
- The number e is the base of John Napier's natural logarithms created in the 1600s.
The symbols ln(x) mean loge(x).
To experiment with log computation visit
How To Appreciate Logs Without Feeling Out On a Limb.
- It is named for Leonhard Euler who studied it in the 1700s.
- It is
irrational, never a fraction. It is a non-repeating, non-terminating decimal.
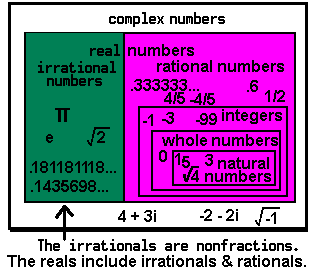
- It is transendental (is NOT a root of a non-zero polynomial equation with rational coefficients).
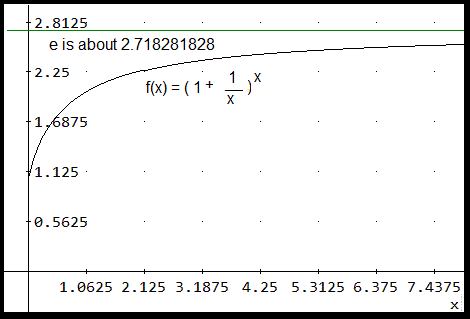
- The first few digits are: 2.718281828459045235360. There is even a
little story to help one memorize the first few digits.
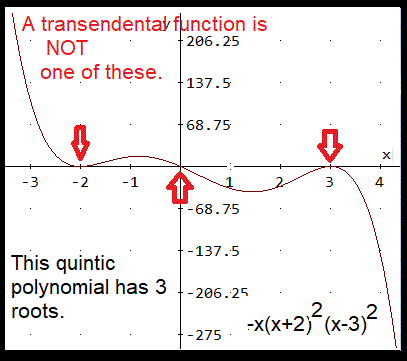
- When used as the base of an exponential or power function, the function's slope works beautifully with the function 1/x, but the value of e is needed. So,
"Solve" for e.
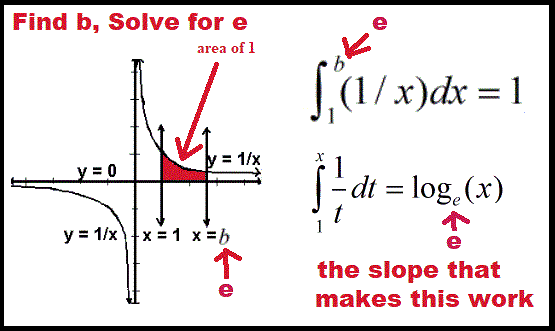
- It is defined, by Jacob Bernoulli in the 1600s, to be the limit, as n goes to infinity, of the nth power of the sum of 1 and the reciprocal of n.
Experiment with this idea by letting t, P0, and r equal 1 and changing n. The larger the n, the closer the limit is to e.
- It may be approximated with this infinite sum. The larger the n, the closer the sum is to e.
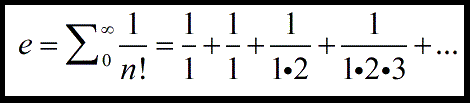
- When used as the base of an exponential or power function, cx where c > 0 and c
 1, it becomes ex. See
An Exponential or Power Function. 1, it becomes ex. See
An Exponential or Power Function.
- If e is the base of a power function, the function, its slope function (derivative), and its area function (integral) all the same. In
"Parent Functions, Their Slope Functions, and Area Functions" see
The Exponential Function, exp(x) or ex
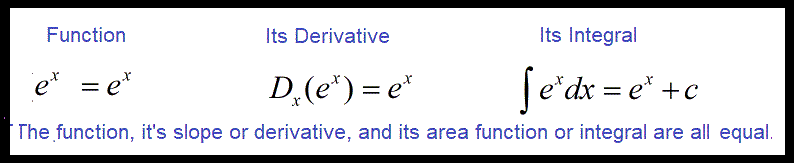
- If e is the base of the log, ie. it is ln(x), the derivative is the reciprocal function. The antiderivative of the reciprocal, x>0, is the natural log.
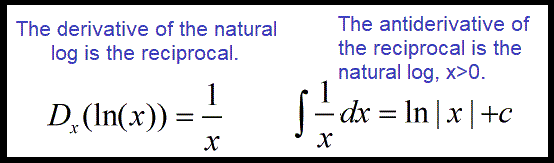
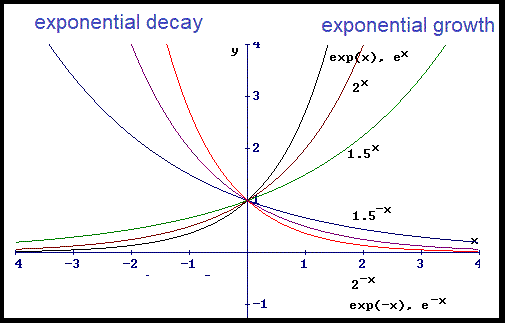
- It is used when modeling
continuous growth and decay.
Experiment with it.
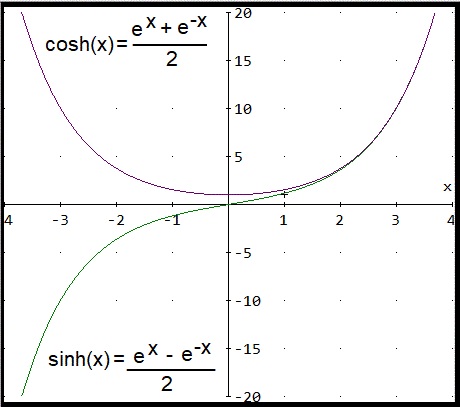
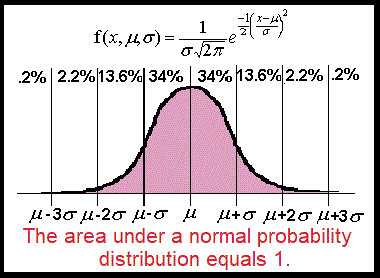
- It is also used in probability to write the
normal distribution, and and trig to write hyperbolic functions,
 |
 |
| Examine the normal, logistic, and exponential functions with a
spread sheet.
|
|



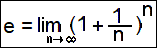
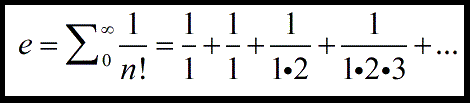
 1, it becomes ex. See
An Exponential or Power Function.
1, it becomes ex. See
An Exponential or Power Function. 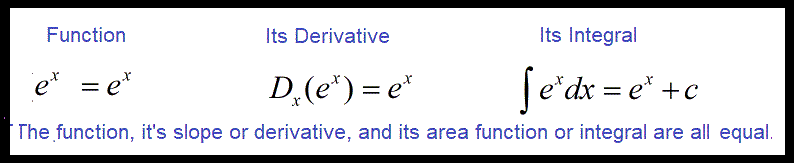
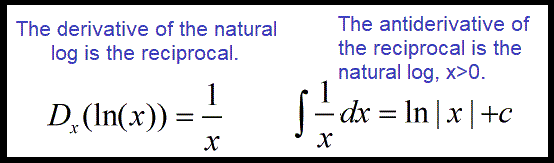






![[MC,i. Home, site home page]](http://www.mathnstuff.com/math/spoken/here/1gif/mcihome.gif)

![[master list of all MSH! dictionary words]](http://www.mathnstuff.com/math/spoken/here/1gif/words.gif)

![[Good Stuff -- free & valuable resources]](http://www.mathnstuff.com/gif/goods.gif)


