Function and Relation Library

Exponential or Power Functions     A Bit about e, the base of the Natural Logs    

The Exponential Function

EXPONENTIAL or POWER FUNCTIONS
• y = b^x, raise the number b to the x power.
• opposite function: y = - b^x
• reciprocal function: y = b^{- x}
• inverse function: y = log_bx
• slope:   y = b^x(ln b)
• ex. y = 2^x

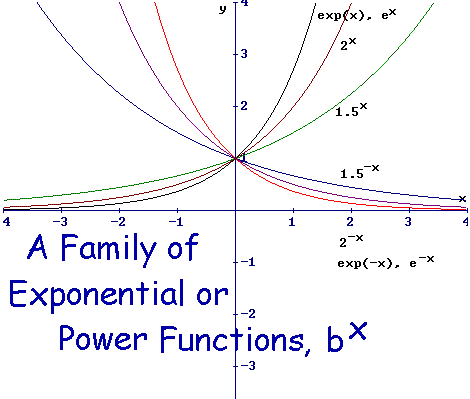
    The doubling function, for example, is a power function.

    Use the rule: y = 2^x.   Use values of 1, 2, 3, and 1/2 for x and get corresponding values of 2, 4, 8, and 2 for y values.

    Examine the "Family of Exponentials Graphs" to see how different y = 1^x behaves relative to y = 1.5^x, y = 2^x, y = e^x. For every value of x, 1^x is 1, so the function is constant, there is no growth.

    For all bases greater than 1, there is ALWAYS GROWTH, as x increases.

    For all bases between 0 and 1, there is ALWAYS DECAY as x increases.

    For positive values of x, the larger the base, 1.5 versus 2, versus e, the larger the value of the function, y = 1.5^x, y = 2^x, y = e^x, and therefore the steeper the curve, the faster the growth: The larger the base, the faster the growth.

    For negative values of x, the smaller the base, 1.5 versus 2, versus e, the larger the value of the function, y = 1.5^x, y = 2^x, y = e^x, the and the steeper the curve, and the faster the growth: For negative values of x, the smaller the base, the faster the growth.

    The slope of y = b^x is b^x(ln b).

    The inverse function for y = b^x is y = log_b x.

    Power or exponential functions are powerful tools. They are used to express growth and decay. They are used to express other function such as:

• the normal distribution (the bell curve in statistics, a dilation and translation of e^-x²/2)
• hyperbolic functions such as
  the hyperbolic sine, sinh x, is (e^x - e^-x)/2,
  the hyperbolic cosine, cosh x, is (e^x + e^-x)/2
• the logistic curve.

    The numbers 0, 1, -1, , e, and i are celebrates among numbers. They are no different than other more common numbers, but are "more famous" and very useful and important. The numbers , 0, 1, and -1 are probably familiar to you. The complex number i is the square root of negative one, -1.   It solves the equation x² = -1 with solutions of i and -i.

    The number e is about equal to 2.71828 but this does not explain what number it is. It also may be said to solve an equation. One definition of e involves the solution of a calculus equation involving an integration, an antiderivative, the inverse of finding the slope.   Here's the equation:

b

(1/x) dx = 1: The integral of the reciprocal from 1 to some upper limit equals one.

1

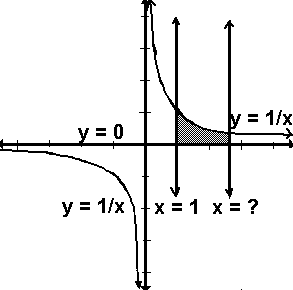
    Consider the graph of the horizontal line y = 0 as a bottom boundary line. Use the vertical line x = 1 as a left boundary line, and the reciprocal function as a top boundary line. A four-sided shape would be created if a vertical line were drawn on the right. The vertical line which creates a shape having an area of one is the vertical line x = e. Suppose the integral of the reciprocal from 1 to some upper limit equals one. That upper limit is e. The number e solves the equation below where the upper limit b is the value being sought.

    You may experiment with this yourself.   Find the upper limit, the value that makes the equation equal to 1.

Solve for b in the equation the integral of the reciprocal from 1 to b equals one. b (1/x) dx = 1 1   1st. Input a value of b to make the result equal to 1.   b= 2nd. Compute . b (1/x) dx = 1   3rd. Try again as needed. The value of e is about 2.71828.

    Ok, so what's the big deal?

    Slope. The exponential function, because of its base e, has the only slope that is the same as the function! The derivative is the same as the function, because the base is e.

THE EXPONENTIAL FUNCTION
• y = exp(x) or y = e^x
• opposite function: y = - e^x
• reciprocal function: y = e^{- x}
• inverse function: y = log_ex or y = ln(x)
• slope: itself, y = exp(x) or y = e^x

    The exponential function is a power function having a base of e. This function takes the number x and uses it as the exponent of e. For values of 0, 1, and 2, the values of the function are 1, e or about 2.71828, and e² or about 7.389056.

    The exponential function is its own slope function: the slope of e-to-the-x is e-to-the-x. The inverse of ex is ln x, which is loge x, the natural logarithm of x.

    Many things are expressed in exponential notation. Growth of the population of people or a disease as well as the decay of a radioactive isotope are expressed in exponential terms. Interest, as in loans or bank balances, if compounded continuously is expressed as a power of e. The true statement e ⁱ - 1 = 0 relates the famous numbers mentioned earlier. Exp(x) or e^x may be computed to desired accuracy knowing that e^x = 1 + x + x2/2! + x3/3! + x4/4! + ...

---

    This page is from Exploring Functions Throught the Use of Manipulatives (ISBN: 0-9623593-3-5).

    You are hereby granted permission to make ONE printed copy of this page and its picture(s) for your PERSONAL and not-for-profit use. YOU MAY NOT MAKE ANY ADDITIONAL COPIES OF THIS PAGE, ITS PICTURE(S), ITS SOUND CLIP(S), OR ITS ANIMATED GIFS WITHOUT PERMISSION.

---

© 2005, Agnes Azzolino www.mathnstuff.com/math/spoken/here/2class/300/fx/library/expofx.htm