Growth, Decay, Loans, Savings
1. In 2000, P(x) = 7,000(1 + 1.5/100)x, was first used to describe the population growth, in years, of Keyport, NJ.
a) What would the population be in 2020 if the growth continues at the same rate.
*9427.985045850375 -- In 2020 the population would be about 9428 people.
P(t) = 7000(1 + .015/1)1*20*
b) Experiment. Use this model to predict about when the population of Keyport will first reach 10,000.
*About 24 years, in 2024 the population would be about 10,007 people.*
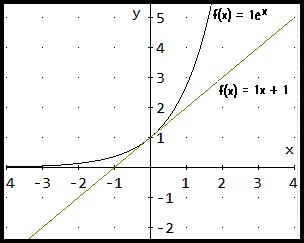
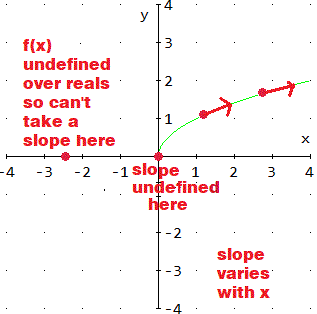
2. The number e is the limit, as n goes to infinity, of (1 + 1/n)n -- as n gets infinitely large.
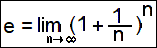

It is approximately 2.718281828459045...
a)What values of P0, r, and t must one use in P(t) = P0(1 + r/n)nt to make it the equation
look like (1 + 1/n)n? *P0, r, and t ust each be 1.*
b) How large must n be to obtain 1 decimal digit of e?
*when n is 75,
the expression equals 2.700378656300911*
c) How many decimal digits of e does the number 10,000 yield?
*If n is 10,000, e is about 2.7181459268249255, so 3 decimal digits.*
3. Half-life means the length of time for half of the substance to decay/be changed.
Radioactive materials decay. Each has its own half-life. For example, Nobelium has a really short half-life of 23 seconds.
See source at:
Physics Application: Radioactive Decay.
a. Find how much 14Carbon, carbon 14, remains after 100 years if 400 mg exists at time 0, and it
DECAYS, at a rate of -.00012097 per year (base e).
*about 395.190 mg.*
b. Find the half-life of 14Carbon. *
P(100) = about 395.190 mg.
P(1,000) = about 354.42 mg.
P(10,000) = about 199.31 mg, too much.
P(5,730) = about 200.00 mg. The half-life is about 5,730 years.*
4. 226Ra has a half-life of 1,620 years and becomes 222Ra upon decay.
Algebraically find its rate of decay. See source at:
Isotopes of radium. *k is about -.00043. * See
work.
5. Which is the better interest? Rate A is 5% nominal interest compounded monthly or
Rate B which is 4% nominal interest compounded monthly? Why is it better?
*Rate A is better. It has an APR of 5.09 %. Rate B has an APR of 4.074 %.*
|

 Starts with a specific amount: b
Starts with a specific amount: b
 Grows the same amount each time (x): m
Grows the same amount each time (x): m
 Used for cost, revenue, and profit functions
Used for cost, revenue, and profit functions

 Used to write the equation for a tangent to a curve
Used to write the equation for a tangent to a curve


 Starts with a specific amount: P0
Starts with a specific amount: P0
 Continuously grows an amount that varies over time
Continuously grows an amount that varies over time
 Approximate e
Approximate e
 Growth, Decay, Loans, Savings
Growth, Decay, Loans, Savings 

 Compounding - Growing Discretely
Compounding - Growing Discretely



 1
1 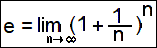

![[MC,i. Home, site home page]](http://www.mathnstuff.com/math/spoken/here/1gif/mcihome.gif)

![[master list of all MSH! dictionary words]](http://www.mathnstuff.com/math/spoken/here/1gif/words.gif)

![[Good Stuff -- free & valuable resources]](http://www.mathnstuff.com/gif/goods.gif)


