


 Slope in Sound & Picture
Slope in Sound & Picture


 Slope in Sound & Picture
Slope in Sound & Picture| Page TOC, Video, & pdf | |
|
Before studying slope, one needs to understand graphing and the coordinate plane. See
A Graph is A Portrait. If you understand these ideas continue. Here are the video and pdf, and Geometer's Sketchpad of/for this page. The page approaches slope in a few ways. These are: VERBAL / Auditory, WRITTEN / Symbolic, PICTORIAL / Visual, CONCRETE / Kinesthetic. VERBAL / Auditory

| |
| History & An Urban Legend |
|
| Renee Descartes and Pierre Fermat (see the Slope Song Sketchpad, sheet 0) are credited with the creation of the coordinate, Cartesian, plane in 1635. Each of the two stories related here involve Renee Descartes. The first is fact. The second is urban legend, believed true but with no documentation or proof as to its validity. As a child, Descartes was sickly an avid scholar and bed-ridden, before becoming a soldier, philosopher ("I think, therefore I am"), mathematician, and teacher. History says he created the coordinate plane for tracking a fly as it crawled about the tiled ceiling above his bed. The urban legend relates the use of the letter, symbol, "m" for slope. Often when one sees a mountain, one thinks of the slope of the mountain. Does the mountain slope up? Does the mountain slope down? Is there a mountain or just a flat plain? Slope has nothing to do with lines or curves but does describe the tilt of a mountain or land. Think of that smart French kid laying in bed then looking out the window at mountains, valleys, plains. He who coordinitized the ceiling might well have coordinaitized the world outside his window, the mountains, the valleys, the plains. The first letter of mountain in French as it is in English is "m." Think "m" for the slope of a mountain. A mountain slope which goes up from a point would be described as a positive slope. A mountain which has a lower altitude as one walks would have a negative slope because the opposite of up is down and the opposite of positive is negative. Think of a flat plain as having no incline. Zero is a logical choice for the slope of land on which one doesn't walk down or doesn't walk up. Between negative and positive in numbers is zero. The "m" for slope story is just an urban legend but the negative for down, zero for flat, and positive for up makes sence for slope. Next see how it might work with sound. | |
| A Slope of Zero |
|
|
Does this sound flat, like a flat plain? The notes/tones/frequencies do not increase (go up) or decrease (go down). It's the same tone repeated. Listen to a slope of one. Then, listen again. The pitch goes higher for each unit of time. We'll use this as the unit of measure of slope. We'll judge other slopes in comparison to this. A free Geometer's Sketchpad! may be downloaded from this link, so the reader can experiment with a slope of 0, seeking where a function is flat or has other values. A number of sheets of ssong.gsp are provided so the reader might become the experimenter and examine slope in the graphs provided. The video might help the reader experiment with functions such as a constant function, a line, a cubic (really good for checking out the slope of hills and finding the flat plain where the slope is zero. Sheets are also included to check out the polynomial and rational functions. One might experiment to figure out the meaning on "no slope" or "undefined" for a vertical line. | |
| The Scale Called Slope |
|
|
You've listened to a slope of one and you've listened to a slope of zero. Using two measurements, a scale or guage is possible. Two measurements are required -- the zero and the one. With these established, other measurements follow. Listen to a slope of zero and to a slope of one.
Before you scroll down on this page, press RELOAD or REFRESH on your browser so the next graphic has animation, then, just sit there, examine the graphic, and think about slope.
| |
|
The Slopemeter |
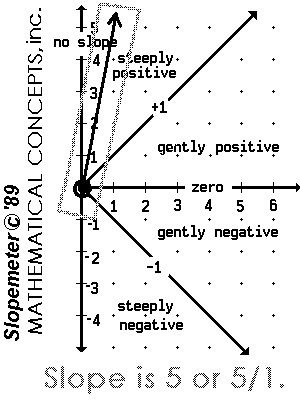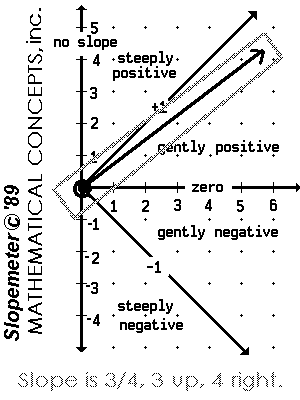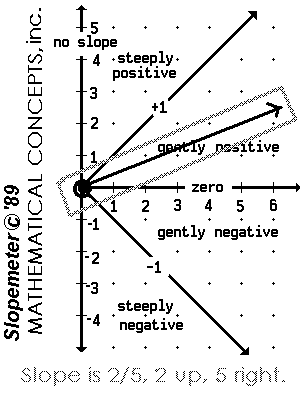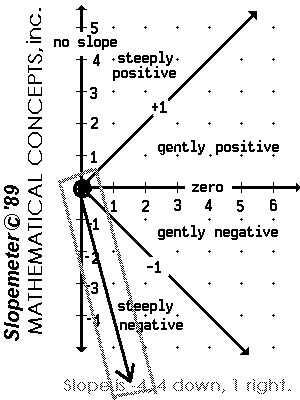
|
| Slope in Sounds |
|
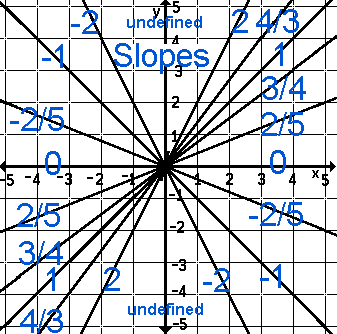
Experiment. Predict the sound of each slope before clicking on the line with the desired slope. | |
| Again
Slope is
Note that the lines and slope above do indeed match. For example:
| |
| Slope As Numbers |
|
|
Experiment. Predict the sound of each slope using the slope of 1 as your standard or unit. Undefined needs clarification. Slope is rise over run. One may rise 5, 4, 6, 10, but because the line is vertical, the run is 0. A constant divided by 0 is undefined. In mountain terms, if one approaches from the bottom of a cliff so steep it can not be climbed, there is no slope because it is very, even infinitly, steep, so, no slope. If one approaches the edge of a cliff from the top, it is a very dangerous drop, so one can not safely descended, there is no slope because one would fall off, so, no slope. Rational functions like 1/x and 1/(x - 3) have x-values where the function is infinitly large. These functions have vertical asymptotes, with a slope of undefined or no slope. There can be no run. There is no slope. If you wish, watch the video and see the last pages of the pdf file. They provide more clarity, if needed or wished.
| |
| Slope -- A Statement of How Are Things Going, A Measure of Change | |
|
Slope still needs clarification. Slope is the rate of change. Slope states in number form how things are going, how fast they are changing and in what direction they are headed. There is even a slope of the slope to state how the change is changing. There is even more to learn than all that. Slope is the rate or speed at which the change is happening and the direction the change is going. These facts are already know.
Examples of "Slope is the rate of change" will help. Slope may be used to compare:
| |
| Rise Over Run with Coordinates & Slope of the Tangent |
||||
|
Before formal arithmetic computation of slope, a review of symbols and their meanings is a good idea. A more complete and detailed list of symbols and their meaning is found at: www.mathnstuff.com/ef/wax/symbols.gif. Here's a short but important list.
| ||||
| Asides |
|
|
If you wish to know more about how the sounds on this page were created, read Slope on the HP. To learn how the slope graphic was produced, read Image Map. | |






|