![[Math Spoken Here! Banner]](banner.gif)
So, What's A Fraction? & Zero(s) In Fractions
- pdf of this page
video of this page
-
- What's A Fraction?
- A fraction is a number. It is a number written as the ratio or comparison of two numbers. The top number is compared to the bottom number. The numerator is
compared to the denominator.
-
- What's the Job of the Top Number?
- The number on the top of the fraction is the numerator, the NUMBERER
. It states "how many pieces are involved."
-
- What's the Job of the Bottom Number?
- The number on the bottom of the fraction is the denominator, the NAMER
. It states "the name of the size of the piece." It is the number of equal pieces in one whole."
-
- So, What Is A Fraction?
- A fraction is a number written so as to compare the number of pieces involved to the
number of pieces in one whole.
-
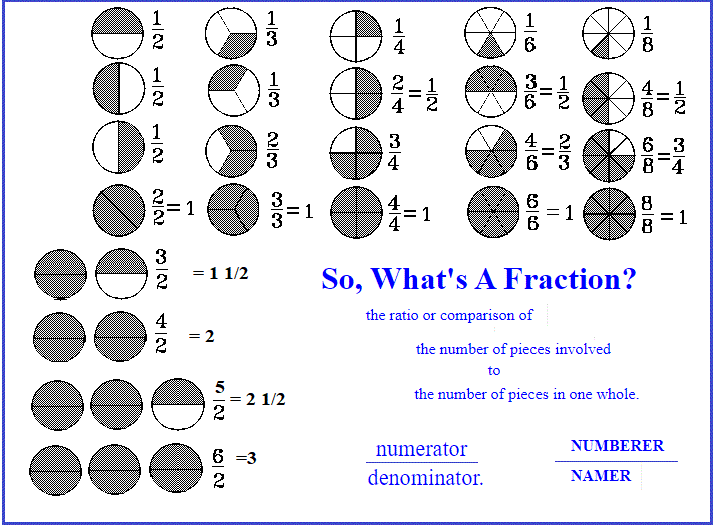
- The fraction one-half, written in symbols as 1/2, means "one piece, where it takes two pieces to make a whole." The fraction a half, written in symbols as 1/2, means
"one piece, where it takes two pieces to make a whole."
- The fraction one-fourth, written in symbols as 1/4, means "one piece, where it takes four pieces to make a whole." The fraction one-quarter, written in symbols as 1/4,
means "one piece, where it takes 4 pieces to make a whole."
- The fraction three-quarters, written in symbols as 3/4, means "three pieces, where it takes four pieces to make a whole."
- The fraction six-eighths, written in symbols as 6/8, means "six pieces, where it takes eight pieces to make a whole."
-
- When Are Two Different Fractions Equal?
- Two fractions are equal when they name the same number. It is often the case that two fractions are equal. One-half (1/2) names the same number as two-quarters
(2/4), or as three sixths (3/6), or as four-eights (4/8). Three-fourths (3/4) is equal to six-eights (6/8) because they are different ways of expressing the same number.
-
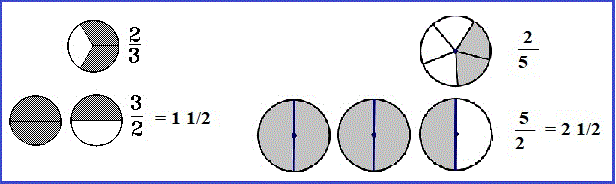
- Does It Really Matter Which Way You Write The Fraction?
- Yes!
Examine the two examples below. It must be written "number of pieces / number of pieces in one whole."
-
-
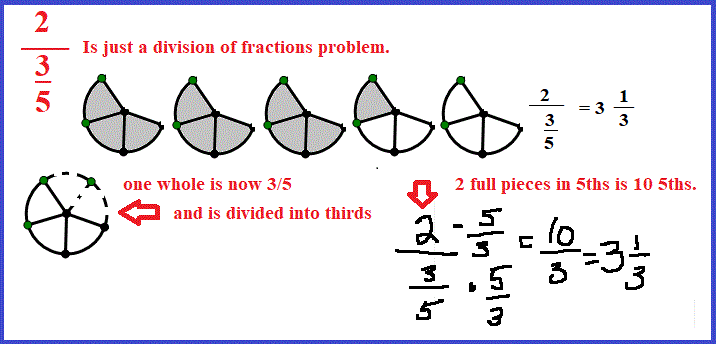
- What Does Mean If You Have a Fraction In the Fraction?
- It is called a complex fraction and is still "number of pieces / number of pieces in one whole."
- For example, below, the denominator, number of pieces in one whole, is now a fraction. So one whole is really 3/5.
-
-
-
- What Does Mean If You Have a Zero in a Fraction
- It will be one of these three kinds of expressions and these depend on where the zero(s) are.
-

- 0/c, where c is a non-zero constant, equals 0.
-
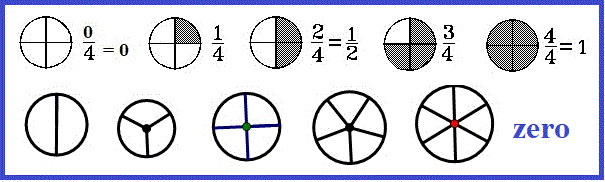
- * It is zero pieces and any non-zero number in one whole.
- * For example, 0/5 = 0, 0/2 = 0 -- 0 pieces and some number of pieces in one whole.
- * 0/c is found in everyday computation. It is just plain zero.
- c/0, where c is a non-zero constant, is UNDEFINED.
- * "You can't divide by 0." There is no computation rule, as one might find for
fractions, for division by zero. Division by zero is NOT DEFINED.
- * c/0 is probably first found in middle school when learning
order of operations and getting ready for computation in which c/0 has a useful meaning.
- * That happens in computing the
slope of a
vertical line
-
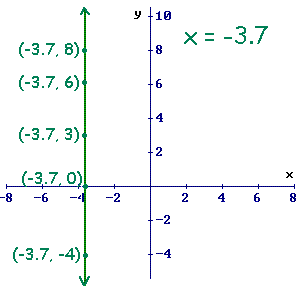
- * c/0 is the reciprocal 0, of 0/c. One might examine 2/0 in a few different ways.
- A. using the function 2/x in the graph below;
- B. in
limit.gsp for taking a limit;
- C. using the picture below and the definition of fraction as discussed above, "number of pieces" /"number of pieces in one whole"
- D. using the calculator on this web page. Try a few numbers. Don't forget to try 0 to see what this html math function says.
-
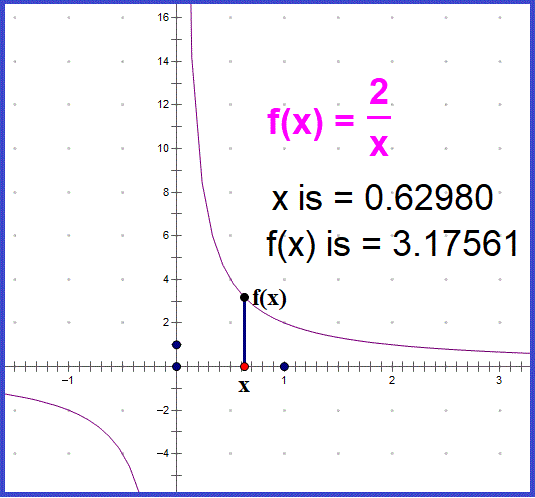
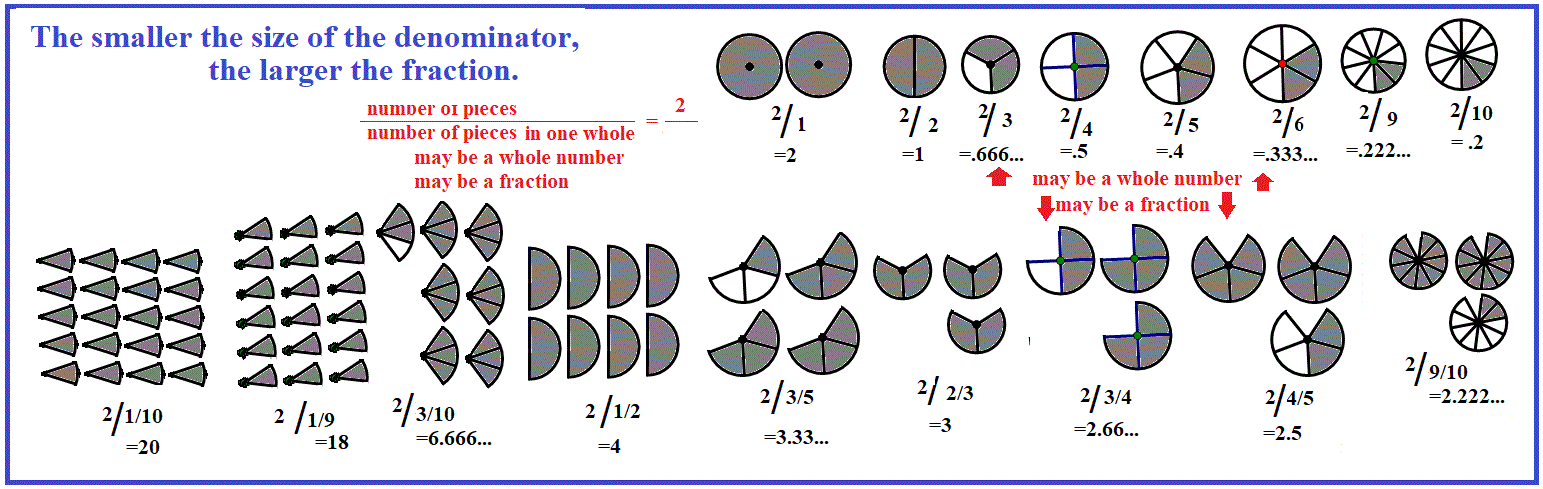
-
- 0/0 is INDETERMINANT.
- * A number of expressions are called INDETERMINANT, meaning the value of the number can not be DETERMINED as is.
- * The expressions are:
0/0, 0x, ∞ , ∞ /∞ , - ∞ , ∞ 0, 00, 1∞
- * A student probably first sees the fraction 0/0 in calc I when studying limits.
- * Here are some examples of
Special Limits. In each case f(0) is 0/0, INDETERMINANT.
- * For more on indeterminant forms see:
https://calcworkshop.com/limits/limits-indeterminate-forms/ and
https://byjus.com/maths/indeterminate-forms/#definition.
This is an edited version of a page from the dictionary MATH SPOKEN HERE!, published in 1995 by MATHEMATICAL CONCEPTS, inc., ISBN: 0-9623593-5-1.

![[MC,i. Home]](//www.mathnstuff.com/math/spoken/here/1gif/mcihome.gif)
![[MSH! Home]](//www.mathnstuff.com/math/spoken/here/1gif/mshhome.gif)
![[Table]](//www.mathnstuff.com/math/spoken/here/1gif/table.gif)
![[Words]](//www.mathnstuff.com/math/spoken/here/1gif/words.gif)

![[this semester's schedule w/links]](//www.mathnstuff.com/gif/semestr.gif)
![[Good Stuff -- free & valuable resources]](//www.mathnstuff.com/gif/goods.gif)
![[next]](//www.mathnstuff.com/math/spoken/here/1gif/next.gif)
![[last]](//www.mathnstuff.com/math/spoken/here/1gif/last.gif)
|
© 2005, 2022, Agnes Azzolino
www.mathnstuff.com/math/spoken/here/3essay/eso.htm
|




![[Math Spoken Here! Banner]](banner.gif)




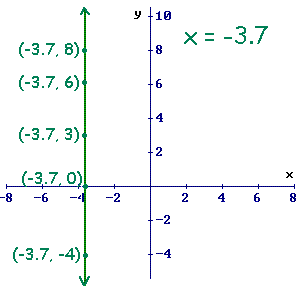



![[MC,i. Home]](http://www.mathnstuff.com/math/spoken/here/1gif/mcihome.gif)
![[MSH! Home]](http://www.mathnstuff.com/math/spoken/here/1gif/mshhome.gif)
![[Table]](http://www.mathnstuff.com/math/spoken/here/1gif/table.gif)
![[Words]](http://www.mathnstuff.com/math/spoken/here/1gif/words.gif)

![[this semester's schedule w/links]](http://www.mathnstuff.com/gif/semestr.gif)
![[Good Stuff -- free & valuable resources]](http://www.mathnstuff.com/gif/goods.gif)
![[next]](http://www.mathnstuff.com/math/spoken/here/1gif/next.gif)
![[last]](http://www.mathnstuff.com/math/spoken/here/1gif/last.gif)