Order of Operations is the Grammer of Mathematics.

Order Makes A Difference in Results

The results are poor if you put your sock on after you've put your shoe on. It is necessary to put your sock on first. The order in which the two actions are performed makes a difference in the result of the activity. The order in which operations or actions are completed makes a difference in the result in mathematics also.

Take a number...

"Take a number, square it, add two to the result" is symbolically written "x² + 2."

"Take a number, add two, square the result" is symbolically written "(x+2)²" or "x² + 4x + 4."

a number, y = x	a number, y = x
a number squared, y = x²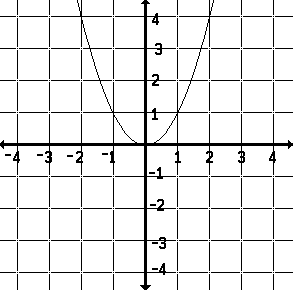	a number increased by 2, y = x + 2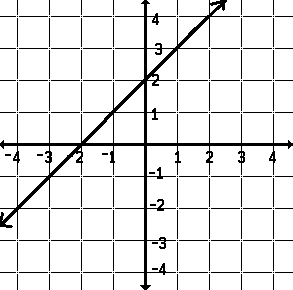
a number squared then increased by 2, y = x² + 2	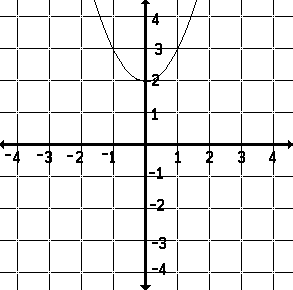a number increased by 2 then squared, y = (x + 2)²

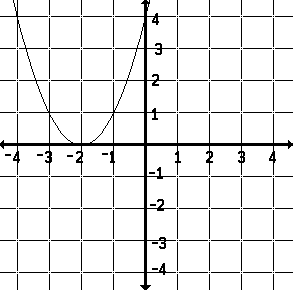x	x² + 2	(x+2)²
-4	18	4
-3	11	1
-2	6	0
-1	3	1
0	2	4
1	3	9
2	6	16
3	11	25
4	18	36

One can see a difference.

Simplifying 3 + 4 · 5: My Dear Aunt Sally

Mathematicians know the order in which operations are performed. Simplify the expression 3 + 4 · 5. If each operation is completed in order, from left to right, 35 results. If multiplication is performed before the addition, recognizing the ordering mathematicians use, 23 results. The expression 3 + 4 · 5 equals 23. Some young math students are taught the phrase "my dear Aunty Sally" to remind them that multiplication or division (prioritized from left to right) is completed before the addition or subtraction (also prioritized from left to right) is completed in an expression.

Please, My Dear Aunt Sally

More sophisticated students use parentheses or marks of inclusion! Inclusion marks:

• set off or isolate an expression within an expression and
• permit prioritizing in an expression.

Though 3 + 4 · 5 is 23, (3 + 4) · 5 means 7 · 5 or 35. Here the addition has precedence over the multiplication: the parentheses indicated this.

The marks of inclusion are:

• brackets: [ ]
• braces: { }
• parentheses: ( ) and the
• bar: &hibar as used in fractions, division problems and roots.

First, Please Readily Excuse My Dear Aunt Sally

First, Please Readily Excuse My Dear Aunt Sally sums up the priorities in a pleasant way.

1st: Functions -- other than those listed here

2nd: Parentheses or other marks of inclusion -- Innermost first!

3rd: Exponents or Roots

4th: Multiplication or Division -- Leftmost first!

Last: Addition or Subtraction -- Leftmost first!

This is a page from the dictionary MATH SPOKEN HERE!, published in 1995 by MATHEMATICAL CONCEPTS, inc., ISBN: 0-9623593-5-1.   You are hereby granted permission to make ONE printed copy of this page and its picture(s) for your PERSONAL and not-for-profit use.

© 2005, Agnes Azzolino www.mathnstuff.com/math/spoken/here/3essay/eooo.htm