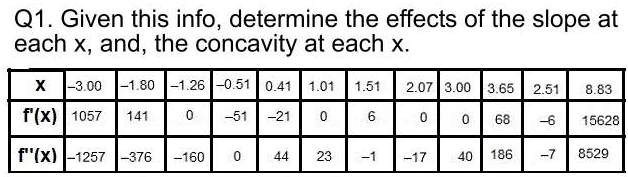
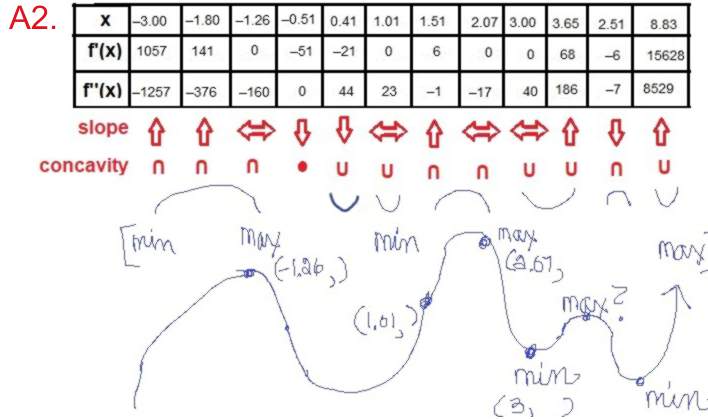
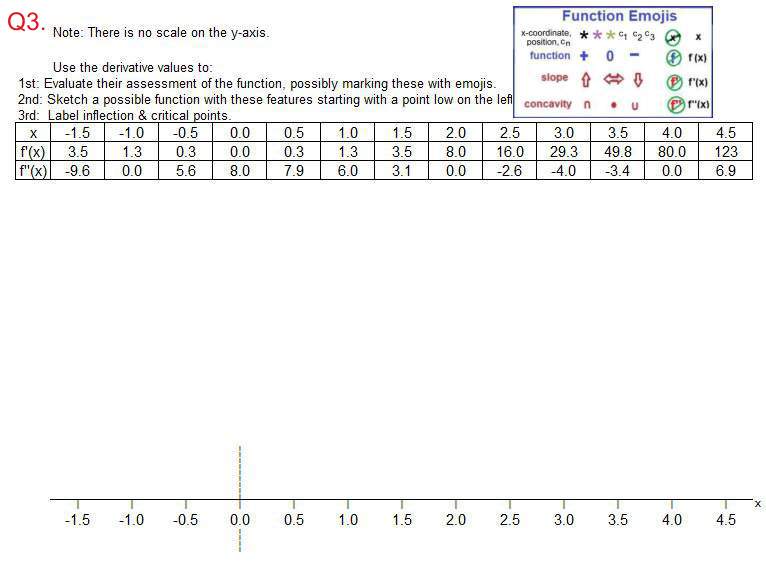
Instructions
- Edit a function as desired or use the one already on the sheet.
- Draw the blue dot on the x-axis to the desired position and note the change in x, function, derivative, and second derivative values.
- Select appropriate emoji(s) and move the emoji(s) to mark a desired characteristic of the function.
Examples and a practice sheet follow. Enjoy.
| | function, then some derivatives |
|
| x |
none |
f |
f, f' |
f, f', f'' |
all |
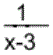 |
none |
f |
f, f' |
f, f', f'' |
all |
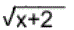 |
none |
f |
f, f' |
f, f', f'' |
all |
|
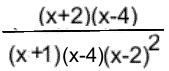 |
none |
f |
f, f' |
f, f', f'' |
all |
|
|