discontinuity

IN MATH: 1.n. a break or missing point in the graph of a function. EX. The curve f(x) = sin(x)/x has a discontinuity when x is 0. See below.

IN ENGLISH: 1. as defined above.

Among Basic Functions

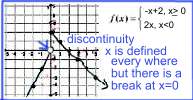
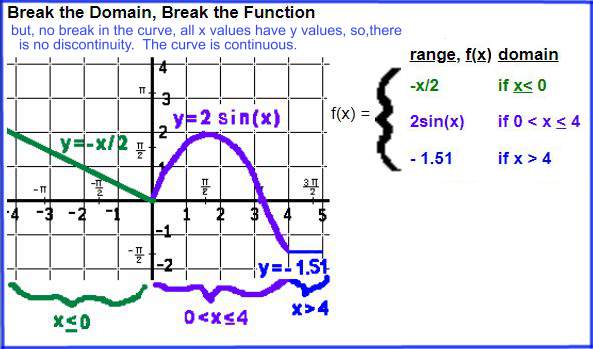
Among the basic functions, the greatest integer functions and reciprocal functions are the only ones with a discontinuity.

The discontinuity in the reciprocal function f(x) = 1/(x+2) is because one may not divide by 0 and that would happen if x equaled -2. The line x = -2 is a vertical asymptote so the curve is "broken" there.

With the greatest integer function, there are multiple discontinuities. A discontinuity exist everytime x is an integer. For x values greater than or equal to the integer, the graph goes on the "higher step." For x values less than the integer, the graph goes on the "lower step."

Continuous Or Not Continuous

Two piece-wise defined functions are illustrated here.

On the top graph, when x equals 0, the right half of the curve does not watch up with the left part of the curve. There is a discontinuity.

On the bottom graph, even though the entire function is defined with 3 seperate functions, the pieces all match and create a continuous though "bumpy" curve.

In Precalculus

In precalc, one learns about polynomial function and rational function. Polynomial functions are always continuous.

Rational functions often have discontinuities. Rational functions, a polynomial divided by a polynomial, a fraction with a polynomial in the numerator and in the denominator, have discontinuities. Since one cannot divide by zero, a zero in the denominator is "not legal" and results in a vertical asymptote. If the function has the same factor in the numerator and denominator a "hole" or missing point discontinuity exists.

In Calculus I

In calc I, the first topic is limits. In studying limits one considers the limit, as x goes to zero, of sin(x)/x, written as
lim_x
0(sin(x)/x).
Though the limit from above and from below 0 is equal to 1, the fraction sin(x)/x when x is 0 is 0/0, an indeterminant form. You have probalby never heard of indeterminant form and might want to check out What Does Mean If You Have a Zero In the Fraction? included in the essay "So, What's A Fraction."

$[MC,i. Home]$ $[Table]$ $[Words]$ $Classes$

[Good Stuff -- free & valuable resources]

$[next]$ $[last]$