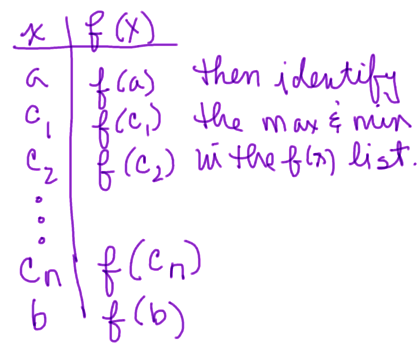
I. Determine/find maximums and minimums.

(Find extrema, the max & minimum y-values.)

1st: (Just so you don't forget to check function values for

      endpoints a and b.)

      Compute f(a) and f(b).

2nd: Find the critical numbers.

      a. Compute f'(x).

      b. Set f'(x) = 0.

      c. Solve to find c₁, c₂, ..., c_n

      d. Organize your result in a table.

3rd: Find possible max & min values.

      a. Compute and list f(c₁), f(c₂), ..., f(c_n).

      b. Scan the f(x) values for the maximum and minumum.

    The value of x or t states the now, the current time or number.
      The f(x) or f(t) states the status at the current time or number.
      The f'(x) or f'(t) states how thing are going, the rate of change, positive (increasing), negative (decreasing), or 0 (no change at the moment).
      The f''(x) or f''(t) states how the change is changing, is the present and future "looking up," (concave up), or at this instant and in the future are things "looking not as positive," (concave down), or things might be changing from "looking up" to "looking down." or from "looking not so positve" to "looking up," because there is pause, 0 change in the change, at this instant.
      The F(x) or F(t) states the overall effect of f(x) or f(t) either as a function or over the interval [a, b] as a number. F(x) is called the antiderivative of f(x).

    Again, x states now,
      f(x), the function value, states the current status,
      f'(x), the first derivative, states how thing are changing,
      f''(x), the second derivative, states how thing are in general and how the change is changing.
      The F(x) or F(t) states the overall effect of f(x) or f(t).

• Mean.Rolle.f'(x).f''(x).gsp - - interval, critical values, maximums, minimums, function emoji, Mean Value and Roll's Theorems, derivative tests,