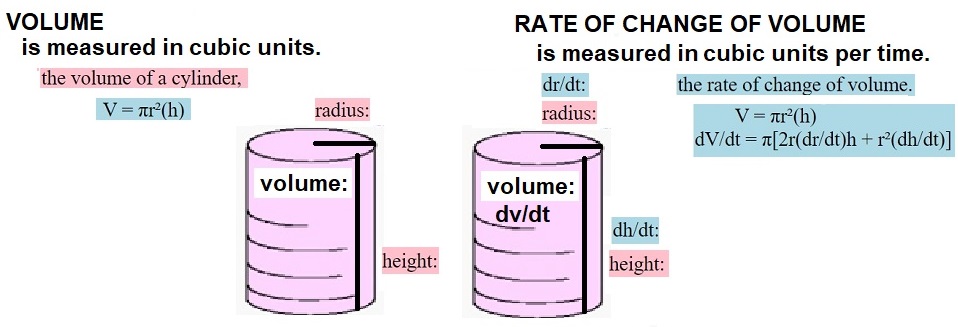
| Things Included in a Situation (Related) & How They Might Change (Rates)
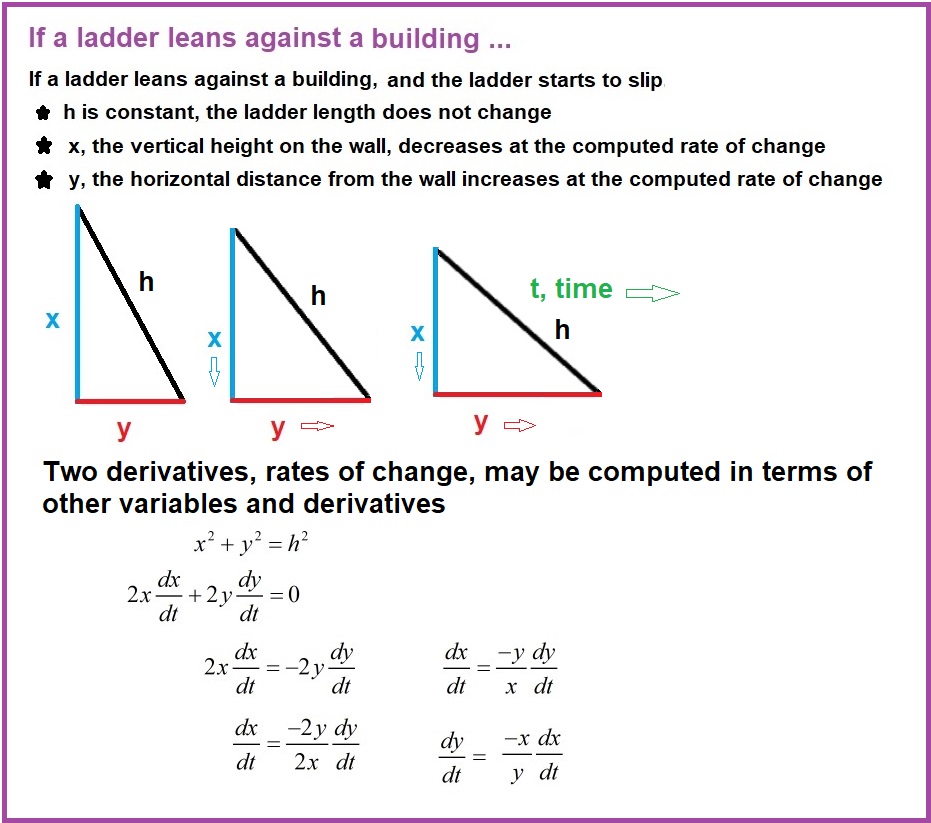
Elementary and high school provided work with circles (with radius, diameter, π), spheres (with radius, π, that fraction 4/3), boxes (with length, width, height, volume, area), right triangles (with legs, hypotenuse) for everyday use. The sides, angles, lengths, were related to each other in specific situations, but, their values didn't change. In each problem change or movement was never considered, because, nothing changed. With the power of implicit differentiation, situations in which a set or collection of things -- constants, functions -- that relate to each other may be considered as changeable. A change in one thing, changes the other things or some of the other things. To experiment visually with related rates, use elevation.gsp It plays with ladders w/h(x), y(x), and h(y), x(y), and h as variable, and h as a constant |
| Symbols & Uses
What was just a number in high school and elementary school, might be a function in college.
| ||||
|
How to Approach the Situation
|
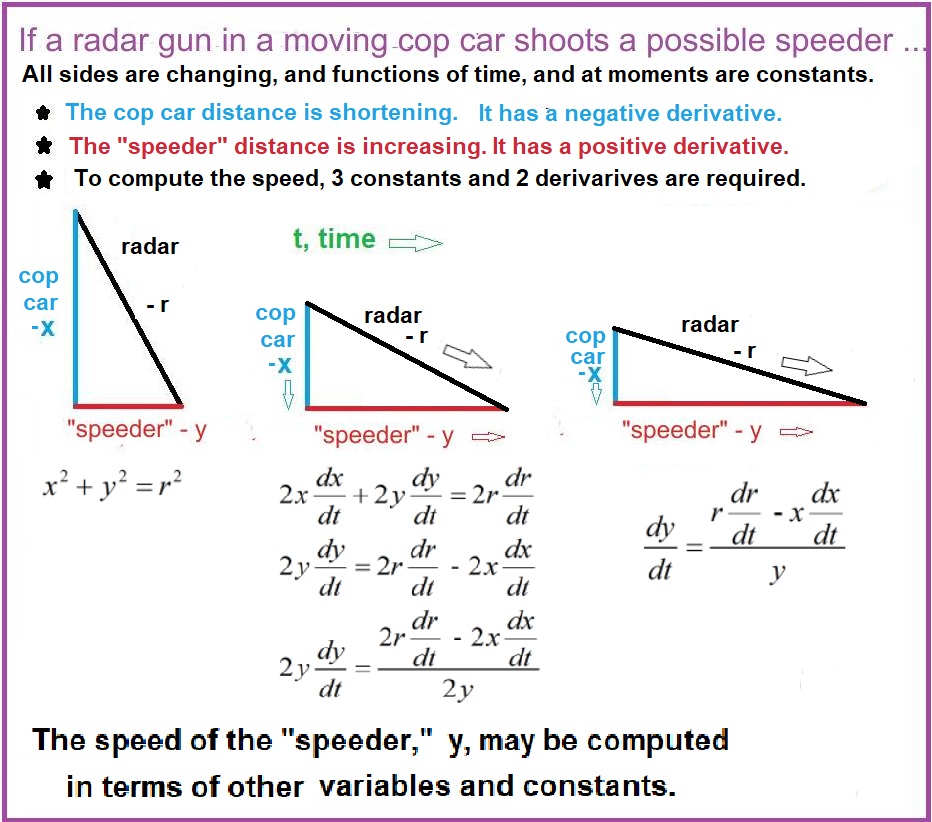
Some Examples Click to enlarge.



| Off-Site Resources
Visit: Paul Dawkins Calculus I, tutorial.math.lamar.edu. |

mathnstuff.com/math/spoken/here/2class/420/related.htm |
|
|