Implicit functions are those which are not directly expressed but are expressed in terms of other functions and independent variables.

    Implicit functions are usually stated as an equation in which one cannot solve for one (or any) function.

    Implicit means
        kind of already know -- Michelle
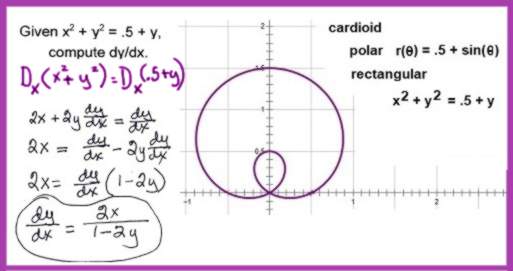
        implied, not stated -- Luna

    As with other functions, one may "take" a derivative of each side of the equation but before that plan your attack.

1. Consider which derivative symbol is cleanest, easiest?
               d(left function)/dx = d(right function)/dx       or
               D_x(left function) = D_x(right function)
   Consider which function and derivative symbols are cleanest, easiest?       f(x) & f'(x),   y & y',   y & dy/dx,   or y & D_x(y).
   A sample is provided below to help you make your decision.
2. Determine which letters stand for variables and which represent functions. The symbol dy/dx is read "the derivative of y with respect to x" so, y is a function and x is the independent variable.
3. Say y is a function in x, y=f(x). Count the y's in the original equation.
4. Each of the original y's requires a dy/dx once the derivative is taken.
5. Isolate all the dy/dx on one side of the equation.
6. Solve for the dy/dx as one usually solves an equation.
7. When taking a second derivative, dy/dx may be part of the solution to the second derivative. If dy/dx is algebraicaly "clean and simple," use the "clean & simple" version in your solution rather than the dy/dx symbol found by taking the first derivative.