MIDDLE GROUND - Binomial Distribution Examples

 

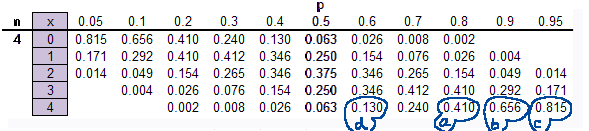
Binomial Distribution Problems         1. State the probability of 0, 1, or 2 successes on 6 independent trials where the probability of success is .3.   2. The probability of producing a perfect drill is .95. If 5 drills are chosen at random, what's the probability that: a. exactly 3 are perfect? b. exactly 4 are perfect? c. 3 or more are perfect?   3a. Suppose 4 students each have about an 80% average in the course so far. Assume this means the probability of maintaining or improving their average is .8. What's the probability that all 4 will maintain or improve their average?   3b. Suppose 4 students each have about an 90% average in the course so far. Assume this means the probability of maintaining or improving their average is .9. What's the probability that all 4 will maintain or improve their average?   3c. Suppose 4 students each have about an 95% average in the course so far. Assume this means the probability of maintaining or improving their average is .95. What's the probability that all 4 will maintain or improve their average?   3d. Suppose 4 students each have about an 60% average in the course so far. Assume this means the probability of maintaining or improving their average is .6. What's the probability that all 4 will maintain or improve their average?   4. A unfairly weighted coin is flipped 9 times. If the probability of obtaining a tail when the coin is flipped is only .2, state the probability of obtaining exactly 3 tails.   5. What's the probability of getting fewer than 3 tails on 9 trials with p(tail)=.2?  Using the table from problem 4.   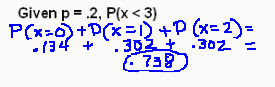6. Given a binomial distribution where n=20, p=.4, state p(x=4).   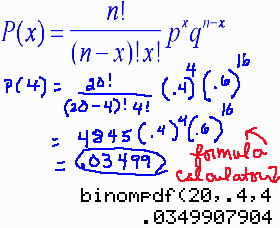7. Suppose 14 students each have a .6 probability of passing statistics. What's the probability that 3 or more will pass?

 

 

© 2010, Agnes Azzolino www.mathnstuff.com/math/spoken/here/2class/90/binom5.htm