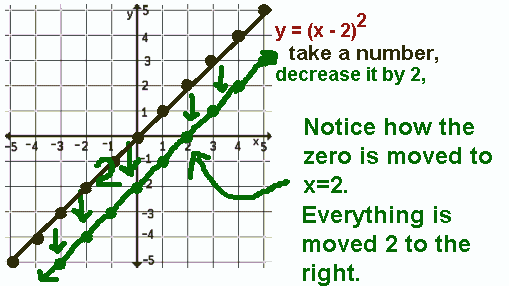
"Domain Shift" Again
But WHY does a "DECREASE in the x-value cause the function, and therefore the
curve, to move to the RIGHT?"
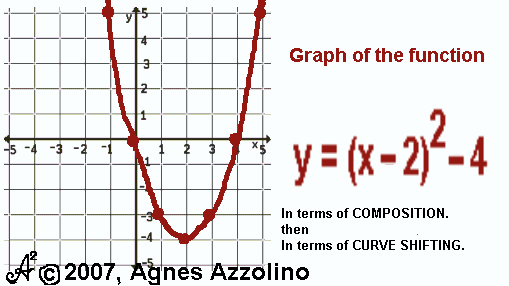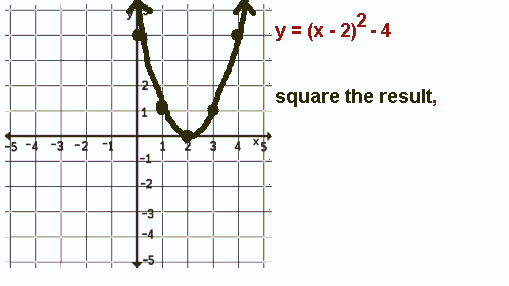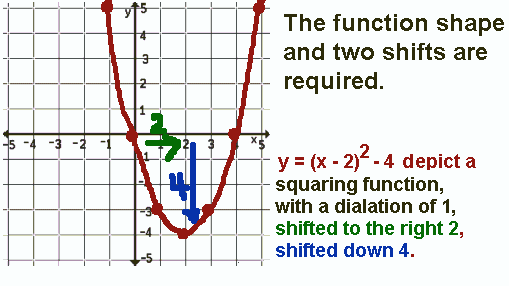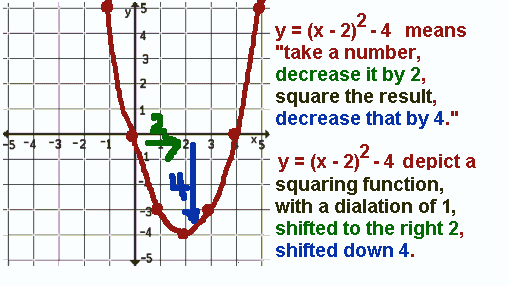
In the function y=(x-2)², x² is shifted to the right.
In the function y=(x+2)², x² is shifted to the left.
All this happens because the value that is squared -- the value the squaring
function uses as its input or domain -- is what determines the value that is output, the function value,
the y-value.
Recall that a
function is a really dependable rule.
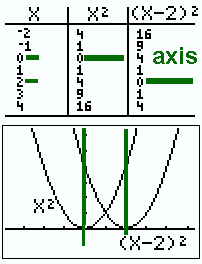
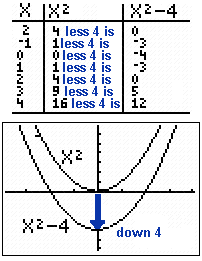
Look above and see that when you square 0, you get
0, when you square -1 you get 1, when you square 1 you get 1, when you square 2 you get 4, and so on --
the usual ..., 9, 4, 1, 0, 1, 4, 9, ... pattern in the output or function or y-values.
Look below and see how INCREASING the x by 2 before squaring moves the
numbers to be squared to LEFT and DECREASING the x by 2 before squaring moves the numbers to be
squared to the RIGHT.
Look for the zeros to see how clearly this shift is visible.

Shortly, the last long animation on this page shows the
composition and how the domain and the range shifts work. Understanding
composition of functions is really important.
| 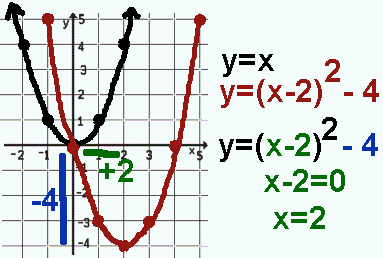





![[MC,i. Home]](http://www.mathnstuff.com/math/spoken/here/1gif/mcihome.gif)
![[Table]](http://www.mathnstuff.com/math/spoken/here/1gif/table.gif)
![[Words]](http://www.mathnstuff.com/math/spoken/here/1gif/words.gif)

![[this semester's schedule w/links]](http://www.mathnstuff.com/gif/semestr.gif)
![[Good Stuff -- free & valuable resources]](http://www.mathnstuff.com/gif/goods.gif)