library

  Function and Relation Library

  Three Most Important Functions:

     Identiy,   Opposite,   Reciprocal


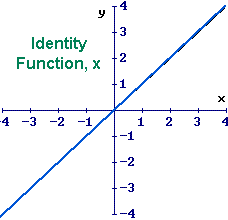
    This is the most important functions. The rule it describes is as follows: use the x value as the y value. The x and the y value in each ordered pair are identically the same, hence, it is called the identity function.

    Experiment with this yourself. Enter a number here: . (Enter negatives as "-x" rather than "- x.") Press: . The value of the identity function for your number is: .

    It is linear. It is a first degree polynomial because it may be written as y = x or where n the exponent is 1 and a the coefficient is 1.

    Its slope is 1 because the coefficient of the x term is 1. Its reciprocal is 1/x. It is its own inverse: the inverse function for y = x is y = x.

    The identity function may be thought of as the basis for all other functions. The linear function y = x + 3, or just x + 3, may be thought of as the sum of the identity function, x, and the constant function 3. The linear function y = 4x, or just 4x, may be thought of as the product of the identity function, x, and the constant function 4. The quadratic function y = x², or just x², may be thought of as the square of the identity function, x · x, or xx, or x².

1.   The identity function uses the x value as the y value: y = x.
Complete each ordered pair using the identity function.
Your answer:         
Answer:
2.   Open an Excel® spreadsheet and save it as math.xls.
Create a column of numbers with the following features.
a.) As the top value in the column, write x, the symbol for the identity function. The symbol x is also used to indicate the first number of an ordered pair.
b.) Let other values in the column be negative and positive constants of your choice.
    Ordering the numbers from smallest to largest is a good idea.
c.) Save this work.


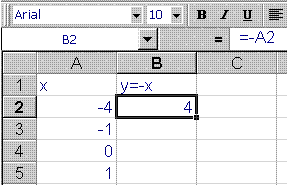
    The opposite function returns the opposite of whatever number is operated upon. If one takes the opposite of a positive, the result is negative. If one takes the opposite of a negative, the result is positive. The opposite of zero is zero.

    Experiment with this yourself. Enter a number here: . (Enter negatives as "-x" rather than "- x.") Press: . The oposite of your number is: .

    It is linear. Its slope is -1. Its reciprocal is -1/x. It is its own inverse: the inverse function is -x.

    Graphically the opposite is useful in reflecting a curve about a vertical axis or a horizontal axis.

The function of the opposite, f(-x),
reflects the function about a vertical axis.
The opposite of the function, -f(x),
reflects the function about a horizontal axis.
3.   The opposite function uses the opposite of the x value as the y value: y = -x.
Complete each ordered pair using the opposite function.
Your answer:         
Answer:
4.   In the Excel® spreadsheet, math.xls, created in question 2, above, create a table of numbers in the column just to the right of the x column, the identity function column.
a.) As the heading for the column, write y=-x, the y value is the opposite of the x value.



    THE RECIPROCAL FUNCTION
  • y = 1/x or y = x-1 y=anxn when an = 1 and n = -1
  • opposite, additive inverse: -1/x
  • multiplicative inverse, reciprocal: x
  • slope: ln x, the natural log of a number
  • inverse function: itself, 1/x

    The reciprocal function returns the reciprocal, multiplicative inverse of the whatever number is operated upon. The reciprocal of i is i. The reciprocal of -1 is -1. Because division by zero is undefined, the reciprocal of zero is undefined: the graph of y = l/x has a vertical asymptote of x = 0. The reciprocal of 2 is 1/2. The reciprocal of 1/2 is 2.

    Experiment with this yourself. Enter a number here: . (Enter negatives as "-x" rather than "- x.") Press: . The reciprocal of your number is: .

    The slope of the reciprocal function is -1/x². It is its own inverse: the inverse of the reciprocal function is the reciprocal function.

    It is a hyperbola, asymptotic to both the x- and y- axes. The reciprocal plays an important role in the creation of other functions. When a function increases, its reciprocal function decreases. When a function achieves a minimum, its reciprocal achieves a maximum. The reciprocal of the sine function is called the cosecant. A reciprocal function is a factor of each rational function.
sketchpad sketchpad
Visit the Interactive Sketch Pad Material
On Reciprocal Functions
  • recipfx   -- graph of parameter-defined reciprocal function,
        * with slide-able tangent line,
        * VERTICAL ASYMPTOTE MUST BE POSITIONED BY USER!


    This page is from Exploring Functions Throught the Use of Manipulatives (ISBN: 0-9623593-3-5).

    You are hereby granted permission to make ONE printed copy of this page and its picture(s) for your PERSONAL and not-for-profit use. YOU MAY NOT MAKE ANY ADDITIONAL COPIES OF THIS PAGE, ITS PICTURE(S), ITS SOUND CLIP(S), OR ITS ANIMATED GIFS WITHOUT PERMISSION.
[MC,i. Home] [Table] [Words] Classes [this semester's schedule w/links] [Good Stuff -- free & valuable resources] [next] [last]
© 2005, 2019, Agnes Azzolino
www.mathnstuff.com/math/spoken/here/2class/300/fx/library/most.htm