-
The Data Is Centered About the Mean-Mode-Median
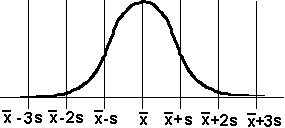
-
- All normal distributions "look like" the one above.
- The mean-mode-median is in the center.
- It is the mean because it is the ARITHMETIC average of all the scores.
- It is the mode because of all the scores the mean score happens MOST often.
- It is the median because when the scores are displayed from lowest to highest, the mean
is the MIDDLE score, the median.
- The EXPECTED value is the mean.
- The frequency curve is bell shaped.
- The bell shape has perfect
bilateral symmetry - the left balances
exactly with the right.
- The score at -2 is balanced by a score at +2 and the frequencies from 0 to +2 and from 0 to -2 are equal.
- The area under the curve from 0 to +2 is exactly the same as the area under the curve from
0 to -2.
- Fifty percent of the scores are above the mean and 50% are below the mean.
- The probability a score is above the mean is 50% and the probability a score is below the mean is 50%.
- Most of the scores are in the middle, about the mean, and few are in the tails, at the extremes.
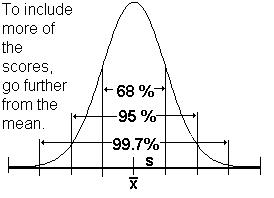
- The area under the curve is equal to 1.
- The probability of an event that does not happen is 0.
- The sum of the probabilities of all events is 1.
- The standard deviation tells one how the scores are spread out and therefore the fatness or
skinniness of the bell.

- Because "the shape" of one normal distribution is "the shape" of all others, the spread of the area of
one normal distribution "is the same" as all others and the standard deviation is the scale.
- The frequencies for the set of scores with a normal distribution are stated by a function which
includes as controlling features both the mean, µ, and the standard deviation,
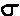 , of the set of scores. , of the set of scores.
That function is:
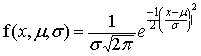
|

 (answers)
(answers)
![[next]](http://www.mathnstuff.com/math/spoken/here/1gif/next.gif)
![[last]](http://www.mathnstuff.com/math/spoken/here/1gif/last.gif)


![[next]](http://www.mathnstuff.com/math/spoken/here/1gif/next.gif)
![[last]](http://www.mathnstuff.com/math/spoken/here/1gif/last.gif)

 (answers)
(answers)
![[next]](http://www.mathnstuff.com/math/spoken/here/1gif/next.gif)
![[last]](http://www.mathnstuff.com/math/spoken/here/1gif/last.gif)

![[MC,i. Home]](http://www.mathnstuff.com/math/spoken/here/1gif/mcihome.gif)
![[Table]](http://www.mathnstuff.com/math/spoken/here/1gif/table.gif)
![[Words]](http://www.mathnstuff.com/math/spoken/here/1gif/words.gif)

![[this semester's schedule w/links]](http://www.mathnstuff.com/gif/semestr.gif)
![[Good Stuff -- free & valuable resources]](http://www.mathnstuff.com/gif/goods.gif)
![[next]](http://www.mathnstuff.com/math/spoken/here/1gif/next.gif)
![[last]](http://www.mathnstuff.com/math/spoken/here/1gif/last.gif)