MIDDLE GROUND
- Number of Ways to Make An Ordered List Or A Group

 

Number of Ways to Create An Ordered List or a Group         These are counting problems. They are used here as an intro to important ideas in probability. They should be considered before reading the page Binomial Distribution.   1. A club has 4 members and wishes to elect a president, vice president, secretary, and treasurer. In how many ways can this be done?       There are 4 ways to select a president, but then only 3 ways to choose the vp, but then only 2 ways to choose the secretary, and then only 1 way to choose the treasurer,         so, there are 4(3)(2)(1) or 24 ways to do this.         Using members A, B, C, and D, here is a tree diagram and the sample space with 24 ways.   2. A club has n members and wishes each member to hold an elected office, beginning with the president, vice president, secretary, and treasurer. In how many ways can this be done?       The answer is n factorial ways. There are n ways to fill the first office, n-1 ways to fill the 2nd office, n-2 ways to fill the 3rd office, and so on. There are n! or n(n-1)(n-2)(n-3) ... (3)(2)(1) ways.   3. A club has 4 members and wishes to elect a president and then a vice president. In how many ways can this be done?       There are (4)(3) or 12 ways to do this.       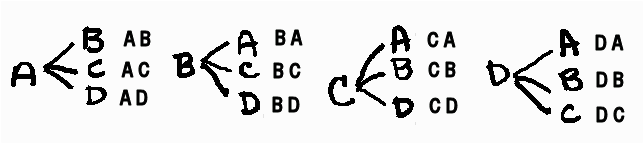Here order counts. A list is required. For a source set of n elements, if order is important and x elements are chosen for the ordered list, a permutation of n things taken x at a time is required, Pn,x. There are n! / (n -x)! ways to do this.       n! Pn,x =   (n-x)!       n!   (number of ordered lists given n things) Pn,x = =   (n-x)!   (shorten the list so only x things are used)         In this problem, an ordered list of 4 elements, take 2 elements is required, P4,2. There are 4! / (4-2)! = 24/2 = 12 ways to do this.   4! 4(3)(2)(1) P4,2 = = = 12   (4-2)! (2)(1)

 

 

Count the Ways       On page Deck of Cards 1 - Counting the Number of Ways An Event Can Occur these problems were completed by simply counting the number of ways. On this page we will use the permutation formula when appropriate. In how many ways can you draw 3 cards without replacement from the face cards? The answer given was: 12x11x10=1320 ways. Using the formula this is:       12!   (number of ordered lists given n things) P12,3 = =   (12-3)!   (shorten the list so only 3 things are used and 9 are unused) In how many ways can you draw 3 cards with replacement from the face cards? The answer given was: 12x12x12=1728. You can not use a permutation to do this problem because cards are replaced.     In how many ways can you draw 5 cards without replacement from the deck of red cards? The answer given was: 26x25x24x23x22=7893600 ways. Using the formula this is:       26!   (number of ordered lists given n things) P26,5 = =   (26-5)!   (shorten the list so only 5 things are used and 21 are unused) In how many ways can you draw 2 cards from the full deck without replacement? The answer given was: 52x51=2652 ways. Using the formula this is:       52!   (number of ordered lists given n things) P52,2 = =   (52-2)!   (shorten the list so only 2 things are used and 50 are unused) In how many ways can you draw all 52 cards from the deck without replacement? The answer given was: 52! 52 factorial ways, 8.0658x10^67 ways. You don't need to use the formula at all, but, you'd get the same answer.       52!   (number of ordered lists given n things) P52,52 = =   (52-52)!   (the list is not to be shortened. All 52 cards are to be used. ) Note: 0! is 1. So 52! / 0! is 52! / 1 or 52!

© 2012, Agnes Azzolino www.mathnstuff.com/math/spoken/here/2class/90/deck3.htm