Use of log-log plane and semi-log plane

    The use of the nonuniform common (base 10) log scale permits detail for a wide range of values.

    Use a semi-log plane to display graphs with an exponential or a power or a large y-range and a small x-range where y-values are all the same sign - negative or positive.

    Use the log-log plane to display graphs were both x-range and y-range vary greatly.

   

Cubing Function, y = x3

Cubing Function, y = x3, on semi-log paper     Note that the extended lines on the y-scale are for powers of 10: 1 or 100, 10 or 101, 100 or 102, 1000 or 103.

Cubing Function, y = x3, other domain values 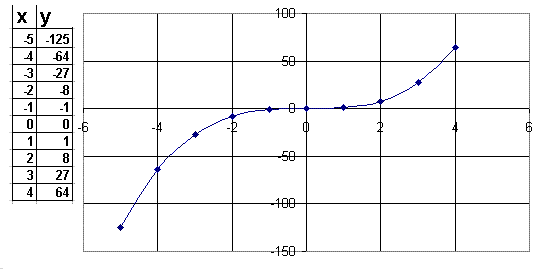    Note that this graph can't be drawn using a log scale because all y values must have the same sign.

The Exponential Function, y = ex     The constant e is the base of the natural log, ln.

The Exponential Function, y = ex, on semi-log plane 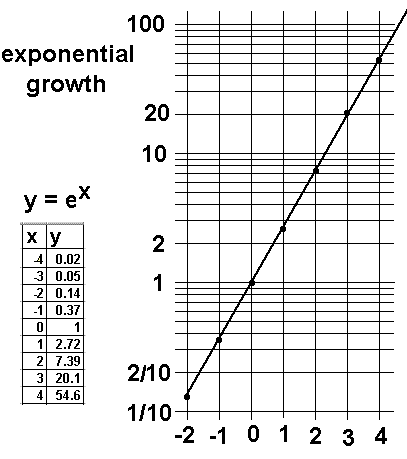    On a semi-log plane, exponential growth is linear.

Exponential & Power Functions, y = abx and y = axm on semi-log plane     Use a graph on semilog or loglog planes to help determine if a function is exponential or power.     On a semi-log plane, exponential growth is linear.     On a log-log plane, a power function is linear and the slope, m, through points (x1, y1) and (x2, y2) is and very like the traditional coordinate plane slope formula.

A Bland Log-Log Plane w/Scales Marked 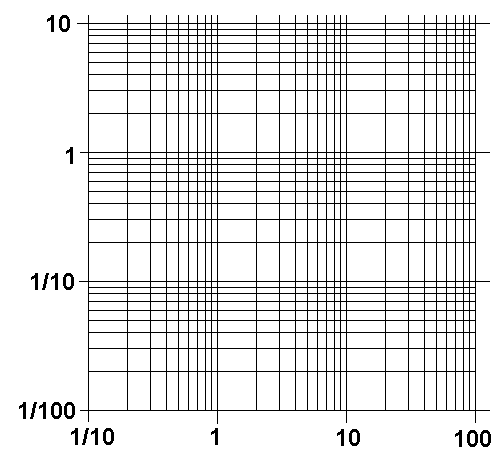    This is an example of how one might vary both scales and still keep accuracy.

© January 25, 2003 85 First Street, Keyport, NJ 07735-1503 www.mathnstuff.com/math/spoken/here/2class/340/loggraf.htm