Imaginary Numbers Are Not Imaginary.

A Number Is an Idea.

A number is an idea. A number is not the written symbol like "5" or the written word "five," it is the idea that is symbolized by "5" or "five." It's something intangible. Something existing only mentally. When we speak or write the number we make it appear more tangible perhaps but it is still only a thought.

The First Numbers

The first numbers were created to answer the question, "how many?" These are the counting or natural numbers. The smallest numbers of this infinitely large set are 1, 2, 3, 4, 5 and 6. Counting numbers also name the sum or product of any two counting numbers. [See NATURAL NUMBER.]

More Numbers Were Created to Express More Sophisticated Ideas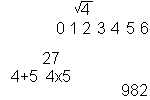

As humans became more sophisticated and needed numbers to express more sophisticated ideas, they created more numbers, more sophisticated numbers. To answer "how many?" when none are present, the number zero, the smallest whole number, is needed. [See WHOLE NUMBER.]

To subtract any two counting numbers, more numbers needed to be created. One can subtract 8 from 10 and name the difference with a counting number, but one cannot subtract 10 from 8 using only counting numbers. To do this integers are needed. The integers include the whole numbers and their opposites. The opposite of 2, -(2), is negative two, -2. Once the idea of -2 exists, one can subtract 10 from 8. The remainder is -2. [See INTEGER.]

Not yet discussed is how one expresses fractional parts. One uses fractions or rational numbers. [See RATIONAL.] These are the quotients of any two integers except that the divisor can not be zero. Three-fourths, 3/4, is legal. Twelve-ninths, 12/9, is legal and equivalent to 4/3 or 1 1/3. Zero divided by 5, 0/5, is legal. It's 0. So is 0/4, 0/29, or 0/57. Each of these is zero. But, 5/0, 4/0, 3/0 and 27/0 are said to be undefined. [See "Undefined Is Not Undefined."]

Espressing Square Roots and Cube Roots

With the above sets of numbers, the naturals, the wholes, the integers, and the fractions or rationals many ideas can be expressed. But not all... With these numbers, one can't express as a single number the "number whose square is 27" or the "number whose cube is 16" even though one could express the "number whose cube is 27" or the "number whose square is 16." Irrational numbers are needed. These are numbers which are not rational, they can't be written as fractions. They are important and necessary to many people, but, they are not fractions. [See IRRATIONAL.]

The square root of 27 is about 5.19615... It can't be written as a rational number, a fraction. It can't be written as a decimal with a last digit. The decimal representation continues infinitely without a continued repetition of digits. The square root of 27 is a number. It is an irrational number.

Of course, we're not discussing irrational in the nonmath context. That irrational means absurd, foolish, or silly. We're discussing irrational in the math context. This irrational means a nonrepeating, nonterminating decimal -- a number which can not be written as a fraction -- a number which is not a rational number.

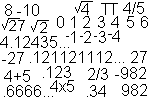
At this point, you may be thinking to yourself, "what an unfortunate name for a number." Years ago negative numbers were called fictitious numbers. That was an unfortunate name but is no longer used. Now however we still use unfortunate names.

All the numbers discussed thus far -- counting, whole, integer, rational, and irrational -- are subsets of the set of numbers called the real numbers. [See REAL.] Yes, there are numbers which are not real.

Imaginary Is Not Imaginary

One can easily express as a single number the "number whose square is 16." The number is 4. Without the imaginary numbers, one can not express as a single number the "number whose square is -4." This number, the square root of negative four, , is an imaginary number. No, not imaginary in the nonmath sense, meaning fictitious or make-believe. The square root of negative four is imaginary in the math sense, meaning a multiple of the square root of negative one.

The first imaginary number is called "i." All other imaginary numbers are multiples of it. "The numbers whose square is negative one" is one way of expressing "i." It makes sense then that should also involve i. The square root of is 2i -- the square root of -1 is i, the square root of 4 is 2.

Imaginaries Are Complex.

The reals and imaginary numbers are subsets of the set called complex numbers. [See REAL NUMBER.] Think of a rectangular coordinate system used to name the points on a plane. Consider the complex numbers a plane. If this is done, the x-axis would be a number line on which might be placed all the real numbers. The y-axis would be a number line on which might be placed all imaginary numbers. Every point in the plane is a complex number, the sum of a real number and a pure imaginary number.

So, imaginary numbers are not really imaginary at all.