|
The numbers  are celebrities among numbers. They are "more famous"
and very useful and important. The numbers are celebrities among numbers. They are "more famous"
and very useful and important. The numbers  are probably familiar
to you. The numbers e and i may not be familiar. are probably familiar
to you. The numbers e and i may not be familiar.
-
![[Hear Word]](//www.mathnstuff.com/math/spoken/here/1gif/hearit.gif) 1, One
1, One
- One is the oldest number. As the smallest counting number it is the number
humans created first. To the Greeks, one was unity for it is a factor of every number.
It the only natural number that is neither prime or composite, because it is unity.
It is the multiplicative identity because the product of one and a number is that number.
One is its own reciprocal. Any number to the power one is that number. So, it is true
that
 . .
-
![[Hear Word]](//www.mathnstuff.com/math/spoken/here/1gif/hearit.gif) 0, Zero
0, Zero
- Zero is the only whole number which is not a counting number. The whole numbers
differ from counting numbers only because of zero. It is the only number that is
neither positive nor negative. It is its own opposite. It is the only number
without a reciprocal, since division by zero is undefined
[see UNDEFINED]. Zero is the additive identity since its sum
with a number is the number.
- Playfully, creatively, using the number 1 and an operations, one might make
the statement: 1 - 1 = 0, thus relating it to another celebrity number.
-
![[Hear Word]](//www.mathnstuff.com/math/spoken/here/1gif/hearit.gif) -1, Negative One
-1, Negative One
- The opposite of one, the additive inverse of one, is negative one. Its product
with a number is the number's opposite. Negative one is its own reciprocal.
- Playfully, creatively, one might make the statement, 0 - 1 = -1
or -1 + 1 = 0, thus relating -1 to two other celebrity numbers and making basic
but important statements as well.
-
![[Hear Word]](//www.mathnstuff.com/math/spoken/here/1gif/hearit.gif) i, The "Imaginary" Unit
i, The "Imaginary" Unit
- The number i, named for the first letter of the word imaginary, is the square
root of negative one,
 . It solves the equation . It solves the equation
 with solutions of i and -i. Each complex number is the sum
of an imaginary number and a real number, a + bi, where a and b are real. With pure
imaginary numbers, a is zero. With pure real numbers, b is zero.
Multiples of i include every pure imaginary number. Powers of i include
only: i, -1, -i, and 1. with solutions of i and -i. Each complex number is the sum
of an imaginary number and a real number, a + bi, where a and b are real. With pure
imaginary numbers, a is zero. With pure real numbers, b is zero.
Multiples of i include every pure imaginary number. Powers of i include
only: i, -1, -i, and 1.
-
![[Hear Word]](//www.mathnstuff.com/math/spoken/here/1gif/hearit.gif)

- The letter pi is the first letter of the Greek word for periphery or
circumference. It is the symbol for the ratio of a circle's circumference to its
diameter. Radian angle measures highlight the importance of this number. The sine
of pi is zero:
 . The cosine of pi is one: . The cosine of pi is one:  .
Because of the periodicity of the circle, the sine, and the cosine, where n
is a natural number, .
Because of the periodicity of the circle, the sine, and the cosine, where n
is a natural number,  . .
-
![[Hear Word]](//www.mathnstuff.com/math/spoken/here/1gif/hearit.gif) e, The Base of the Natural Log
e, The Base of the Natural Log
- The number e is about equal to 2.71828. Leonard Euler conventionalized the
symbol for e as he did for the numbers
 and i. But stating who
chose the symbol does not explain the reason for naming this number in such a manner. and i. But stating who
chose the symbol does not explain the reason for naming this number in such a manner.
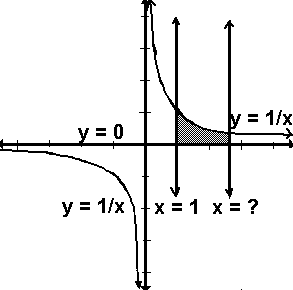 One explanation involves an area. It's an important area because it conveniently
relates logarithmic and exponential functions to rational and polynomial functions.
There are many log and exponential functions because there are many choices for
bases. Ten, the base of our number system, is much too large. Nine, eight, and
six are all too large to make the slope of the reciprocal function equal to a log
function. But, there is a number to serve as a base which makes the slope of the
reciprocal function equal to a log function. The ideal base is the number that
makes the area described below equal to 1.
One explanation involves an area. It's an important area because it conveniently
relates logarithmic and exponential functions to rational and polynomial functions.
There are many log and exponential functions because there are many choices for
bases. Ten, the base of our number system, is much too large. Nine, eight, and
six are all too large to make the slope of the reciprocal function equal to a log
function. But, there is a number to serve as a base which makes the slope of the
reciprocal function equal to a log function. The ideal base is the number that
makes the area described below equal to 1.
-
- Consider the graph of the horizontal line y = 0 as a bottom boundary
line. Use the vertical line x = 1 as a left boundary line, and the reciprocal
function as a top boundary line. A four-sided shape would be created if a
vertical line were drawn on the right. The vertical line which creates a shape
having an area of one is the vertical line x = e. With this number e as the base,
the slope of the reciprocal function is the log function the because e provides
the exact curvature to make that happen. This is really important and useful.
-
- The number e is also useful in writing complex numbers. Using Abraham
DeMoivre's Formula for the computation of complex powers,
 , Euler profoundly stated, , Euler profoundly stated,  . .
-
- With his profound statement four of our celebrity numbers are related.
- The End
- Now, we playfully end this dictionary relating all these celebrity numbers.
 . .
|
 are celebrities among numbers. They are "more famous"
and very useful and important. The numbers
are celebrities among numbers. They are "more famous"
and very useful and important. The numbers  are probably familiar
to you. The numbers e and i may not be familiar.
are probably familiar
to you. The numbers e and i may not be familiar.
![[Hear Word]](//www.mathnstuff.com/math/spoken/here/1gif/hearit.gif) 1, One
1, One
 .
.
![[Hear Word]](//www.mathnstuff.com/math/spoken/here/1gif/hearit.gif) 0, Zero
0, Zero
![[Hear Word]](//www.mathnstuff.com/math/spoken/here/1gif/hearit.gif) -1, Negative One
-1, Negative One
![[Hear Word]](//www.mathnstuff.com/math/spoken/here/1gif/hearit.gif) i, The "Imaginary" Unit
i, The "Imaginary" Unit
 . It solves the equation
. It solves the equation
 with solutions of i and -i. Each complex number is the sum
of an imaginary number and a real number, a + bi, where a and b are real. With pure
imaginary numbers, a is zero. With pure real numbers, b is zero.
Multiples of i include every pure imaginary number. Powers of i include
only: i, -1, -i, and 1.
with solutions of i and -i. Each complex number is the sum
of an imaginary number and a real number, a + bi, where a and b are real. With pure
imaginary numbers, a is zero. With pure real numbers, b is zero.
Multiples of i include every pure imaginary number. Powers of i include
only: i, -1, -i, and 1.
![[Hear Word]](//www.mathnstuff.com/math/spoken/here/1gif/hearit.gif)

 . The cosine of pi is one:
. The cosine of pi is one:  .
Because of the periodicity of the circle, the sine, and the cosine, where n
is a natural number,
.
Because of the periodicity of the circle, the sine, and the cosine, where n
is a natural number,  .
.
![[Hear Word]](//www.mathnstuff.com/math/spoken/here/1gif/hearit.gif) e, The Base of the Natural Log
e, The Base of the Natural Log
 and i. But stating who
chose the symbol does not explain the reason for naming this number in such a manner.
and i. But stating who
chose the symbol does not explain the reason for naming this number in such a manner.
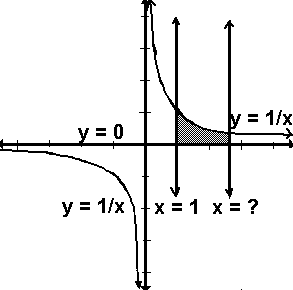 One explanation involves an area. It's an important area because it conveniently
relates logarithmic and exponential functions to rational and polynomial functions.
There are many log and exponential functions because there are many choices for
bases. Ten, the base of our number system, is much too large. Nine, eight, and
six are all too large to make the slope of the reciprocal function equal to a log
function. But, there is a number to serve as a base which makes the slope of the
reciprocal function equal to a log function. The ideal base is the number that
makes the area described below equal to 1.
One explanation involves an area. It's an important area because it conveniently
relates logarithmic and exponential functions to rational and polynomial functions.
There are many log and exponential functions because there are many choices for
bases. Ten, the base of our number system, is much too large. Nine, eight, and
six are all too large to make the slope of the reciprocal function equal to a log
function. But, there is a number to serve as a base which makes the slope of the
reciprocal function equal to a log function. The ideal base is the number that
makes the area described below equal to 1.
 , Euler profoundly stated,
, Euler profoundly stated,  .
.
 .
.
![[Math Spoken Here! Banner]](banner.gif)
![[Hear Word]](http://www.mathnstuff.com/math/spoken/here/1gif/hearit.gif)
![[MC,i. Home]](http://www.mathnstuff.com/math/spoken/here/1gif/mcihome.gif)
![[MSH! Home]](http://www.mathnstuff.com/math/spoken/here/1gif/mshhome.gif)
![[Table]](http://www.mathnstuff.com/math/spoken/here/1gif/table.gif)
![[Words]](http://www.mathnstuff.com/math/spoken/here/1gif/words.gif)

![[this semester's schedule w/links]](http://www.mathnstuff.com/gif/semestr.gif)
![[Good Stuff -- free & valuable resources]](http://www.mathnstuff.com/gif/goods.gif)
![[next]](http://www.mathnstuff.com/math/spoken/here/1gif/next.gif)
![[last]](http://www.mathnstuff.com/math/spoken/here/1gif/last.gif)