Undefined is defined. Define means to set the limits, explain. So, undefine means not to set limits or not to explain.

Sometimes It's Better Not To Say Anything

In society, it is often best not to make a comment: it keeps you out of trouble, it might mean you don't have to tell a lie so someone's feelings aren't hurt. In math, no comment or definition is used for at least two purposes:

• to permit flexibility,
• to avoid confusion because a definition is really beyond the scope of the situation.

This second case is similar to the adult's answer "Because you can't" to the child's question "Why?"

Permitting Flexibility

Earlier in the text is was stated that a number is an idea. It can't be touched, felt, held, seen, but it can be thought. Freedom, love, points, lines, and planes are ideas also. They can't be touched, felt, held, seen, but they can be thought. For centuries, philosophers have asked and other answered the question, "what is love?" For centuries, mathematicians have chosen not to philosophize but to move on. We too shall move on.

"Because You Can't"

Because-you-can't reasons may cause confusion. Such is the case in two instances in mathematics.

The most confusing statements in elementary school mathematics are "You can't divide by zero. Division by zero is undefined." The most confusing statement in high school mathematics is "You can't take the square root of a negative number." What follows is an attempt to clarify why you, or mathematicians, don't divide by zero, and why you, or mathematicians, can take the square root of a negative number. As background, please read "Imaginary Numbers Are Not Imaginary". The point made there is in trying to do something or express something, a new, more sophisticated idea, is created. The idea may be beyond the scope of anyone else other than the thinker. The square root business should, I hope, be cleaned up. The division by zero needs to become clearer. A graph may help.

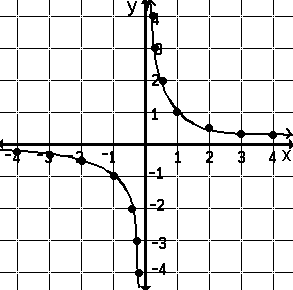
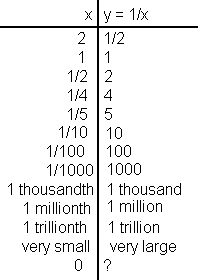
Judging by the table and the graph at the left, as a positive number becomes smaller, and smaller, its reciprocal becomes larger and larger. The closer in size the number is to zero, the larger its reciprocal becomes. If numbers were to follow this pattern, the reciprocal of zero would be infinitely large -- definitely larger than any real number.

To make a definition of division by zero even more unlikely, as a negative number becomes larger, and larger, its reciprocal becomes smaller and smaller (larger and larger negatively). The closer in size the negative number is to zero, the smaller its reciprocal be comes. If numbers were to follow this pattern, the reciprocal of zero would be infinitely small -- definitely smaller than any real number.

There are certainly things humans can think about. Whether division by zero will in future times be defined I can not tell. I do know there is more than one "size of infinity" and that there are mathematicians who work on, think about, the mathematics of the infinite.

This is a page from the dictionary MATH SPOKEN HERE!, published in 1995 by MATHEMATICAL CONCEPTS, inc., ISBN: 0-9623593-5-1.   You are hereby granted permission to make ONE printed copy of this page and its picture(s) for your PERSONAL and not-for-profit use.

© 2005, Agnes Azzolino www.mathnstuff.com/math/spoken/here/3essay/eun.htm