MIDDLE GROUND - Binomial Formula Explained

 

The Binomial Formula Explained         Each piece of the formula carries specific information and completes part of the job of computing the probability of x successes in n independ only-2-event (success or failure) trials where p is the probability of success on a trial and q is the probability of failure on the trial.   P(x)   the probability of x successes in n independent trials     n! n factorial, n(n-1)(n-2)...(3)(2)(1)   the number of ways an ordered list of n items may be formed         n!   (number of ordered lists given n things) Pn,x = =   (n-x)!   (shorten the list so only x things are used)     n!   (number of ordered lists given n things) Cn,x = =   (n-x)! x!   (shorten to only x things)(remove duplicates)     px      the probability of a successes on each of x trials     q(n-x)      the probability of a failure on the remaining trials

 

 

Combinations Compute The Number       of Each Outcome in A Binomial Distribution         Printed in red above and below is the formula for a combination. A combination may be used to compute the number of ways each outcome occurs.     n!   (number of ordered lists given n things) Cn,x = =   (n-x)! x!   (shorten to only x things)(remove duplicates)         A combination takes the number of ways to make an ordered list of n elements (n!), shortens the list to exactly x elements ( by dividing this number by (n-x)! ), and then (by dividing by x!), it removes the number of duplicates.           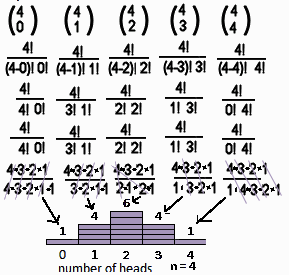Above, in detail, is the combinations and computation required to state for n = 4 trials, the number of times there are 0 heads, 1 head, 2 heads, 3 heads, and 4 heads.         Below are the combinations for n=1, n=2, n=3, and n=5 trials.           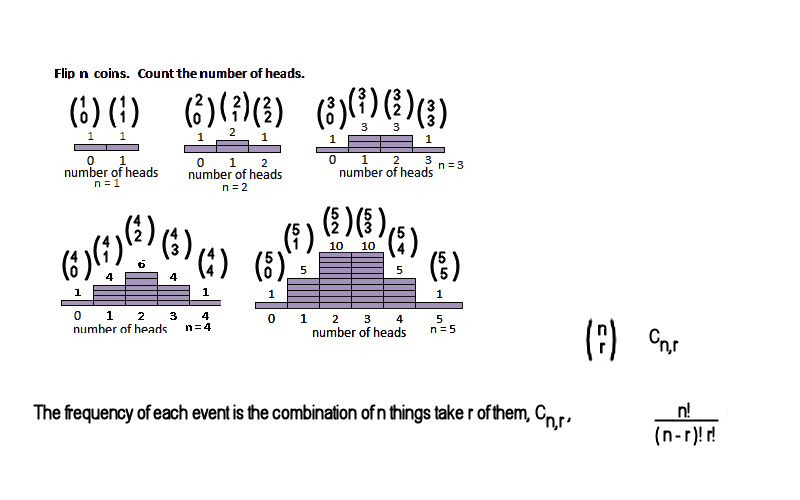The combination function is found in the Math, Probability menu of a calculator.         Combinations are used to compute a term of Pascal's triangle, in statistics to compute the number an events, to identify the coefficients of a binomial expansion and here in the binomial formula used to answer probability and statistics questions.

 

 

One Use of The Binomial Formula         What's the probability exactly 3 heads are tossed if a fair coin is flipped 4 times?         The number of trials, n, is 4. The number of successes, x, is 3. The probability of success, p, is .5 which makes the probability of failure, q, .5.     n!   P(x) = pxqn-x   (n-x)! x!       4!   P(3) = (.5)3(.5)(4-3)   (4-3)! 3!       (4)(3)(2)(1)   P(3) = (.5)(.5)(.5) (.5)   (1) (3)(2)(1)       4   P(3) = = .25   16           This is the same answer found in a binomial distribution table for 4 trials, using 3 successes and a probability of .5, or 1/2, on each trial.           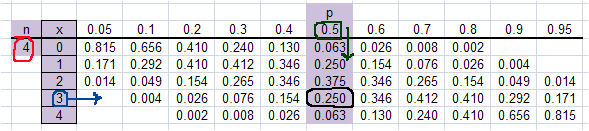The table eliminates the need for the computation and is very useful when more than one problem or a multy step problem is considered.         Before considering the later type of problem, note that the probability of 3 successes in 4 trials, P(x=3), when p is .8 increases to .410 and that with p equal to .1, P(x=3) = .004.

 

 

The Problem Extended         Consider only the experiment flip 4 fair coins and count the number of heads. The probabilities are found in the purple column above where p is .5 and in the table below.      x    0    1    2    3    4 P(x) .063 .25 .375 .25 .063 P(x) 1/16 4/16 6/16 4/16 1/16         State the probabilities using mental math and the table above. It's easier to use fractions and leave the answers unreduced as shown in the table.   1. P(x=3) 2. P(x=1 or x=3) 3. P(x=0 or x=1 or x=2) 4. P(x < 3) 5. P(x > 2)         The answers follow.   1. P(x=3) = 4/16 = 1/4 = .25   2. P(x=1 or x=3) = 4/16 + 4/16 = 8/16 = 1/2 = .5   3. P(x=0 or x=1 or x=2) = 1/16 + 4/16 + 6/16 = 11/16 = .6875   4. P(x < 3)= 11/16 = .6875, the same as question 3   5. P(x > 2) = 11/16 = .6875. Because 2 is the center event and because of the symmetry of a binomial distribution, this probability is the same as P(x < 2) or problem 3.

 

 

Applications         This time you know the answers. The math has already been done. This time the words and translation into the math are the problem.            x    0    1    2    3    4 P(x) .063 .25 .375 .25 .063 P(x) 1/16 4/16 6/16 4/16 1/16         State the probabilities using mental math and the table above. It's easier to use fractions and leave the answers unreduced as shown in the table.   1.      Joan must take a 4-question true-false quiz. If she doesn't even read the questions, what is the probability she will get exactly 3 questions correct?   2.      On the same quiz, what's the probability Joan gets an odd number of answers correct?   5.      On the same quiz, what is the probability she gets 2 or more correct?   3.      A fair wheel has the numbers 1, 2, 3, 4, 5, and 6 marked on its edge. When the wheel is spun one of the numbers is at the top of the wheel. If the wheel is spun 4 times, what's the probability an even number is at the top fewer than 3 times?   4.      Four machines have been poorly built. It's a 50/50 chance that a machine will start when it is switched on. What's the probability that at most half of the machines will run?         The answers follow.   1. P(x=3) = 4/16 = 1/4 = .25   2. P(x=1 or x=3) = 4/16 + 4/16 = 8/16 = 1/2 = .5   3. P(the number is 2 or 4 or 6 fewer than 3 times) =       P(x<3) = 1/16 + 4/16 + 6/16 = 11/16 = .6875   4. P(x < 3)= 11/16 = .6875   5. P(x > 2) = 11/16 = .6875

 

 

© 2011, Agnes Azzolino www.mathnstuff.com/math/spoken/here/2class/90/binom3.htm