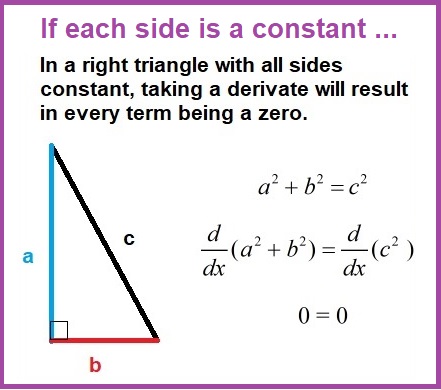
Elementary and high school provided work with circles (with radius, diameter, π), spheres (with radius, π, that fraction 4/3), boxes (with length, width, height, volume, area), right triangles (with legs, hypotenuse) for everyday use. The sides, angles, lengths, were related to each other in specific situations, but, their values didn't change. In each problem change or movement was never considered, because, nothing changed.

      With the power of implicit differentiation, situations in which a set or collection of things -- constants, functions -- that relate to each other may be considered as changeable. A change in one thing, changes the other things or some of the other things.

      To experiment visually with related rates, use elevation.gsp It plays with ladders w/h(x), y(x), and h(y), x(y), and h as variable, and h as a constant

    What was just a number in high school and elementary school, might be a function in college.

The volume of a cylinder V = πr²(h) radius:   units height:   units = cubic units	The rate of change of volume of a cylinder V = πr²(h) dV/dt = π[2r(dr/dt)h + r²(dh/dt)]   radius:   at the given time height:   at the given time dr/dt:   units per unit time dh/dt:   units per unit time   = cubic units = cubic units per unit time

Use elevate.gsp, a Geometer's Sketchpad elevation.gsp -

1 - angle of elevation/depression,

2 - ladder with h(y)

3 - ladder with h(x)

4 - ladder with h is the variable - angle & length may be changed

5 - y is variable, h is constant

6 - x is variable, h is constant

 

Download Geometer's Sketchpad for Free! at http://www.keypress.com/gsp/download

1. Analyse the stationary situation with a picture and one or more equations.
   Note: each letter is a variable unless it is a constant.
2. In a related rate situation, every variable is now a function. So, all the functions are now related because as one function changes the other functions also change.
3. As with implicit differentiation, every y must get a dy/dx, if x is the variable. But now the variable is most likely time, so every y also gets a dy/dt and every x gets a dx/dt.
4. Then when you take a derivative to introduce the related rates (the changes), every variable is a function so it gets a d(variable)/dt.
5. After taking the derivative, plug in all the known constants and rates.
6. Solve for the desired rate even if it means you have a derivative of another function as a variable.

    Visit: Paul Dawkins Calculus I, tutorial.math.lamar.edu.

• Related Rates Worksheet
   
• Related Rates Practice Problems
• Optimization Practice Problems