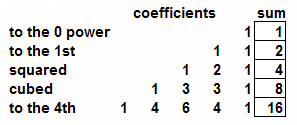| 1a. | How does one square a binomial?
Cube a
binomial? |
| 2a. | What are the coefficients of a binomial squared?
Cubed?
Raised to the 4th power? |
| 3a. | When are we ever going to use this stuff? |
| | |
| 1b. | What does it mean to square a binomial? Cube a
binomial? |
| 2b. | Why is the sum of the coefficients of a binomial raised
to the nth power the same as 2n? |
| 3b. | What patterns do you see in binomial expansions and what
causes each pattern? |
Which set of questions do you prefer to answer, the first that focuses on what
or the second that focuses on why?
Don't bother choosing, answer both. Use both points of view. Let the how
explain why. Think not just "What is the pattern?" but also "Why is that the pattern?"
It all starts with multiplication.
Qu. 1. Expand (x-y)², the square of the difference between two numbers.
Qu. 2. Expand (x-y)³, the cube of the difference between two numbers.


New material begins now.
- 3a. When are we ever going to use this?
- Binomial expansion and Pascal's Triangle are extremely important for
two reasons.
- Pattern recognition, expression, and verification IS the "job" of mathematics.
Techniques, skills, insights, and the mathematics learned here are LIFE SKILLS not just stuff
used to learn the next new topic.
- Recognizing an expanded binomial, factoring it, is a skill required in precalc, calc I, calc II, calc III
in polynomial and rational number expression and graphing, in finding maximums and minimums and
extrema, and in Taylor and McLauren expansions.
- 3b. What patterns do you see in binomial expansions and what causes each pattern?
-
- An extensive collection of the patterns is found on the page
"Binomial Expansion Presented Symbolically and Pascal's Triangle,"
but, it is not meant to be an exhaustive list. Students should be encouraged to seek, express, and verify
other patterns.
-
- An extensive discussion on combinations is found on the page
"Factorials, Permutations, and Combinations -- Ways of Counting Sets of Stuff"
and additional brief comments are made below.
| Take Your Pick on Focus and Method.
| |
Select 1, 2, 3, or 4 of the next 4 questions. Questions 3 and 5 pose the question in
the more abstract form. Questions 4 and 6, suggest using a graphic summary. One might pose question
3, then use 4 as a hint, then pose question 5. Asked alone, Question 6 prompts visual evaluation and summary.
| Qu. 3. | "Why is the sum of the
coefficients of a binomial raised to the nth power the same as 2n?" |
| Qu. 4. | Given a larger print copy of the graphic below,
linked here,
answer the question: "Why is the sum of the coefficients of a binomial raised to the nth power the same
as 2n?" |
| Qu. 5. | Seek, express, and try to verify some patterns. |
| Qu. 6. | Given a print copy of the graphic below, seek,
express, and try to verify some patterns. |
 |
Click on the graphic for a larger copy. |
| Seek, express, and try to verify some patterns. |
|
 |
Click on the graphic for a larger copy.
- 2a. What are the coefficients of a binomial squared?
Cubed? Raised to the 4th power?
-
- 2b. Why is the sum of the coefficients of a binomial raised to the nth power
the same as 2n?
|
2a. What are the coefficients of a binomial squared? Cubed? Raised to the 4th power?
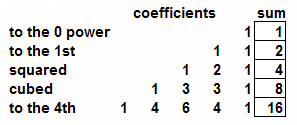
2b. Why is the sum of the coefficients of a binomial raised to the nth power the same
as 2n? Each time a binomial is raised to the next
highest power, the number of multiplications, and therefore terms, is doubled. The doubling function,
2x, is needed. 
3b. What patterns do you see in binomial expansions and what causes each pattern?
- Every term -- as every tile, token, and fold-able manipulative in an expansion -- has the
same degree.
- The number of different kinds of terms -- as different kinds of tiles, tokens, or fold-able manipulatives
in an expansion -- is one more than the degree.
-
- A square, 2nd degree, has 3 terms, 3 different kinds of tiles.
-
- A cube, 3rd, degree, has 4 tokens (or fold-able manipulatives).
- The coefficient of a term states the number of identical products, order doesn't count, though the
foldable manipulative or colored picture illustrates different products where order or orientation does
count.
-
- The coefficient counts the number in the group, hence,
combinations is idea for this purpose.
-

- The degree of a term indicates the "purity" with respect to x and y.
-
- In an expansion of the nth degree:
-
- xn and yn are the "purest."
-
- x(n-1)y1 and x1y(n-1) are the next purest, and so on.
-
- those in the middle (for even degrees) equally mix x and y.
|