|
Turns out COMBINATIONS, the number of possible groups which can be
formed, is the key to simplifying binomial expansion. First, a review of factorials, permutations and
combinations is in order, no pun intended.
Here's the plan for this page.
- Review symbols and vocabulary.
- Examine an example in which listing is the way to determine a count.
- Examine an example in which computation and formulas determine the count.
- Restate the formula for COMBINATIONS.
The reader is again reminded that this is reference material. Tiles and Tokens
are not used or discussed. One might scroll through and continue on to the next page.
| Review symbols and vocabulary. | |
| Constants and Simple Algebraic Expressions |
| n | - | the NUMBER of things all together.
The size of the source set. |
| r | - | the number of things removed
or CHOSEN to form a LIST OR a GROUP. |
| n-r | - | the number of things left after r
things have been chosen or removed. |
| n-r+1 | - | the number "just before" the
number removed when numbers are written in decreasing order.
|
| Factorial | - |
the product of all natural numbers less than or equal to a natural number. It may be UNORDERED, but,
usually when un-computed it is written as a decreasing ORDERED list of factors. The number zero factorial,
0!, is defined to be 1.
1! = 1 2! = (2)(1) or 2
3! = (3)(2)(1) or 6
4! = (4)(3)(2)(1) or 24
0! = 1 by definition
r! = (r)(r-1)(r-2)…(3)(2)(1)
n! = (n)(n-1)(n-2)(n-3)…(3)(2)(1)
n! = n(n-1)(n-2)…(n-r+1)(n-r)…(3)(2)(1)
n! = [n(n-1)(n-2)…(n-r+1)][(n-r)…(3)(2)(1)]
n! = [factors for the r chosen things][factors for the n-r remaining things]
|
| Permutation | - |
an ORDERED LIST of a r things chosen from a source of n things:
1st thing, 2nd thing, 3rd thing, …, nth thing
|
| Combination | - |
an UNORDERED GROUP of a r things chosen from a source group of n things |

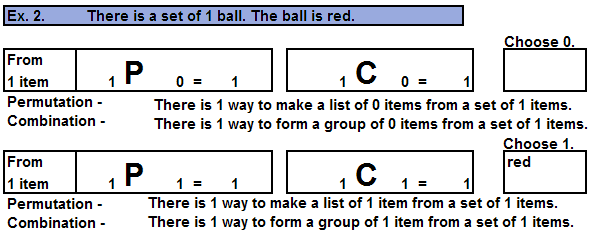
| Listing is a way to determine a count. | |


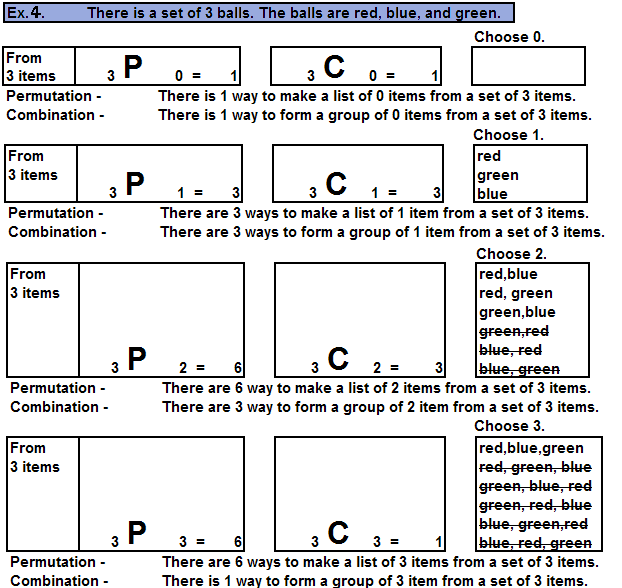
So what is the purpose of the above analysis? It's to find patterns to eliminate
computation required to expand a binomial. Find and verify a pattern and decrease or eliminate long,
messy computation.
| Computation and formulas determine the count. | |
Rather than listing then counting the number of ways a list or group can occur,
as shown above, factorial, permutations, and combinations facititate counting.
Factorial computes the number of ways a list of n things can be made and is
the function or rule which must be used three times to express the desired COMBINATION.
The permutation of n things taken r at a time shortens the list to only r long and
computes that number of ways.
The combination of n things taken r at a time removes duplicates, since order
doesn't count in a group, and computes that number of ways.
Now revisit a problem completed above, using factorials and the formulas for
permutation and combination.

- 3! = (3)(2)(1) or 6
- n! = (n)(n-1)(n-2)(n-3)…(3)(2)(1) or n!
Three factorial, 3!, computes the number of ways a list of 3 things can be made.
There are 3 choices for the 1st in the list, 2 choices for the second in the list, and 1 choice for 3rd in the list:
3! = 3x2x1 = 6.
"N factorial," n!, computes the number of ways a list of n things can be made.
There are n choices for the 1st in the list, n-1 choices for the second in the list, n-2 choice for 3rd in the
list, so on till 3 choices, 2 choices, and 1 choice: n! = (n)(n-1)(n-2)(n-3)...(3)(2)(1).
In order to limit the number in the list to just r things, division by (n-r)! is needed.
This is what the permutation does. Notice that n! is (n)(n-1)(n-2)…(n-r+1)(n-r)! and division by (n-r)! does limit
the list as needed.

The permutation of 3 things taken 2 at a time, 3P2,
computes the number of ways a list of 3 things can be shortened to a list of 2 things and the number of
ways then computed.
Next, it is necessary to remove duplicates. Combinations does this. It takes the
permutation and divides by r! to eliminate duplicates making the count of lists a count of groups.

The combination of 3 things taken 2 at a time, 3C2,
removes duplicates from the list and counts the number of groups of 2 that can be made from a list of 3
things.
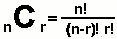 |
Term Tiles and Tokens extend only to the fourth dimension.
On another page, the concrete, manipulative, listing of terms is presented.
For 4th and higher dimensions, combinations, patterns on the next page, and
the expansion formula below are needed.
|
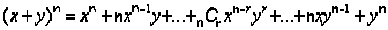
|




