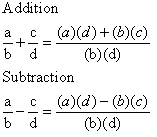Think mental math for easy to add fractions. Think this quick traditional algorithm for work when not emphasizing prime factorization and creating a common denominator. It is used in college-level liberal arts courses and by mathematicians, but, not preached in most US high schools.

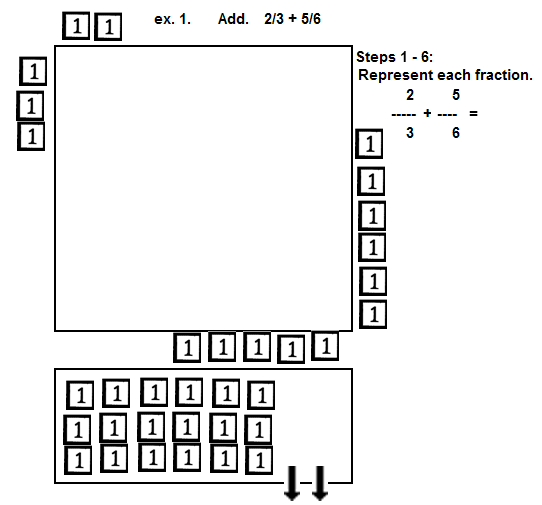
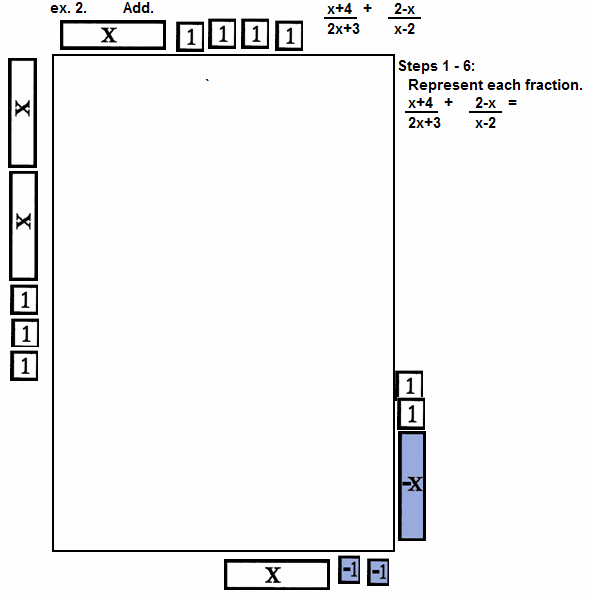
Represent.
0th:	Attempt to mentally add the fractions using equivalent fractions with a common denominator.
1st:	Use two display area. Let the one on the top (further from the user) be for the numerator of the sum. Let the one on the bottom (closer to the user) be for the denominator of the sum.
2nd:	Represent the first numerator in storage on the horizontal on the top left corner.
3rd:	Represent the first denominator in storage on the vertical side on the top left corner.
4th:	Represent the second numerator in storage on the horizontal in the bottom right corner.
5th:	Represent the second denominator in storage on the vertical of the bottom right corner.
6th:	Represent the product of the two denominators in the lower display area in a rectangular array of your choice.
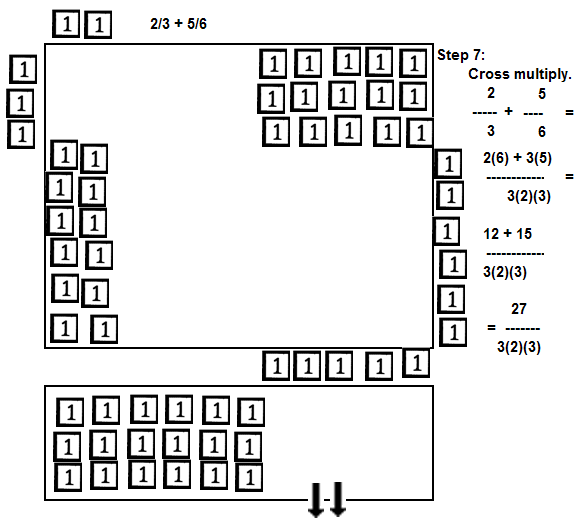
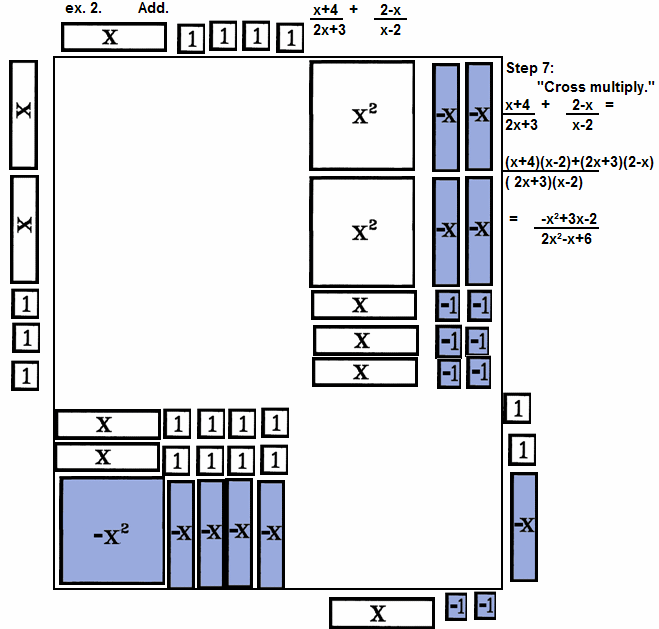
"Cross Multiply."
7th:	"Cross Multiply" each numerator with the other denominator placing the results in the numerator display area.     This means, multiply the (numerator) horizontal from the 1st with the (denominator) vertical from the 2nd, placing the product in the lower left corner.     Then, multiply the (numerator) horizontal from the 2nd with the (denominator) vertical from the 1st, placing the product in the upper right corner.
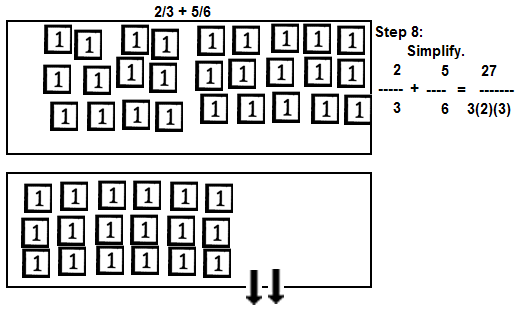
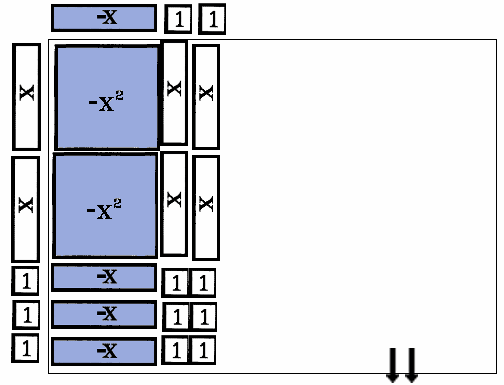
Simplify and Reduce.
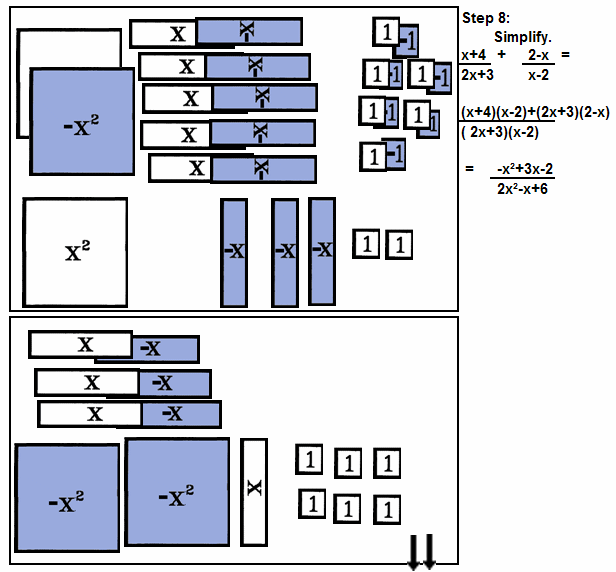
8th:	Simplify the tiles in the numerator display area.
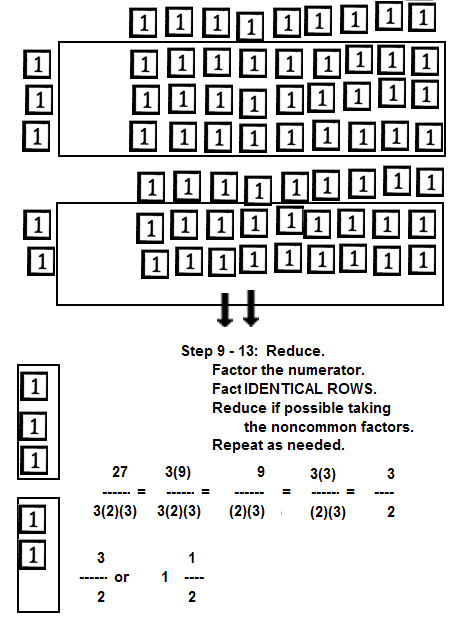
9th:	Remove tiles for both the numerator and denominators VERTICAL AND HORIZONTAL storage areas.
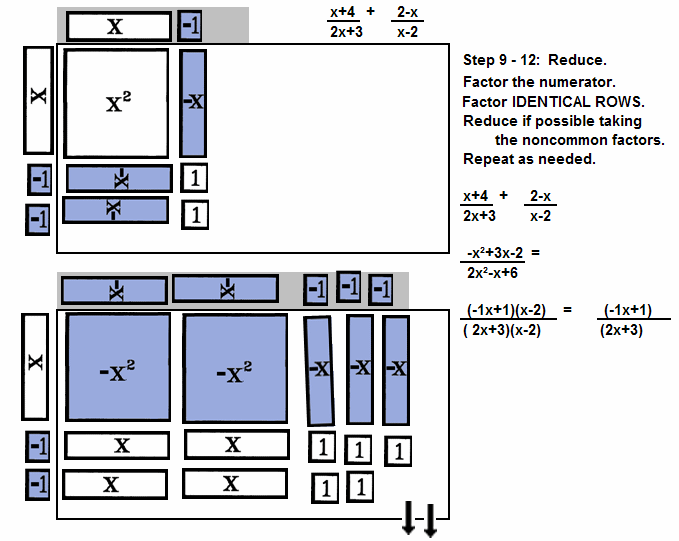
10th:	Factor the numerator, if possible.
11th:	Factor the denominator, if possible.
12th:	Use the factors they don't have in common as the new numerator and the new denominator. Whenever possible, remove a top factor with an identical bottom factor. TO REDUCE, USE THE FACTORS THEY DON'T HAVE IN COMMON AS THE NEW NUMERATOR AND THE NEW DENOMINATOR.
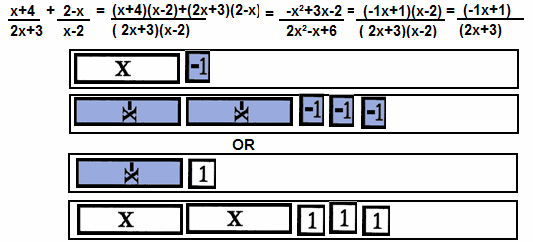
13th:	Repeat steps 9 and 10 and 11 and 12 as often as needed.

      Reducing (a-b)/(b-a) is tough for many students. See "(A-B)/(B-A) is 1." Once the idea is understood, student still forget to look for the short cut of reducing the fraction before computation. Here, we assume the student has not seen the short cut and uses the above algorithm.