Reduce A Fraction in Tilted Array Display.
| 1st: | Arrange the tiles in IDENTICAL rows (or columns),
if possible. The ARRANGEMENT of tilted and nontilted tiles in EVERY row (or every column) must be
IDENTICAL. This will factor out a constant. |
| 2nd: | Remove ALL BUT ONE row (or column) from the display
area to represent the entire reduced fraction. |
| 3rd: | Repeat steps 1 and 2 on the new display of tiles to see if the
reduced fraction may also be reduced. |
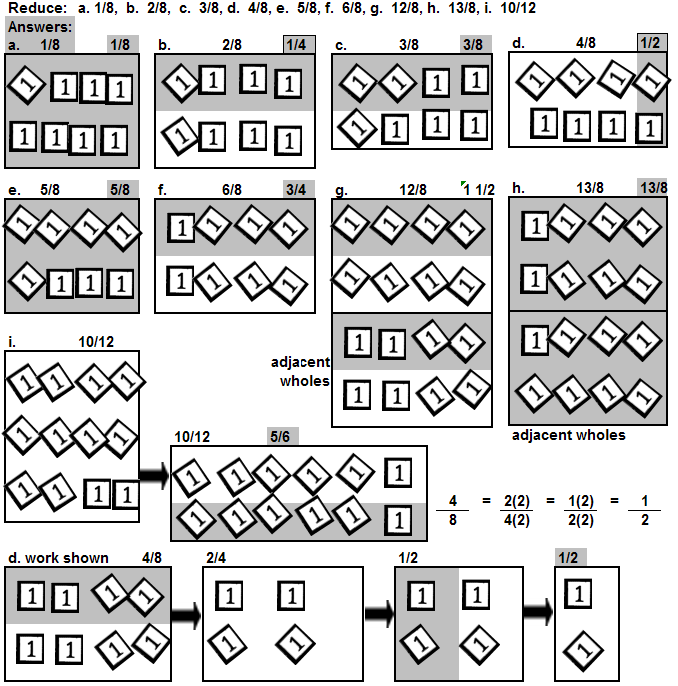
Examine the work above on reducing 4/8. Placing tiles in rows and columns
FACTORS the denominator into a factor pair, (the number of rows) x (the number of columns). Notice that in
the box with 8 tiles, the tiles are in two rows and 4 column (8 = 2 x 4). Because the 2 rows of tiles can be
made, 2 is a factor of the denominator. Because 2 IDENTICAL rows are possible, 2 is a factor of the
numerator. Since 2 is a factor of the numerator and the denominator, the fraction 4/8 is 2/4.
To reduce 2/4, creating 2 identical rows means there is a factor of 2 in the
denominator (because of the rows) and in the numerator (because of the identical). The fraction 2/4 may be
reduced to 1/2.
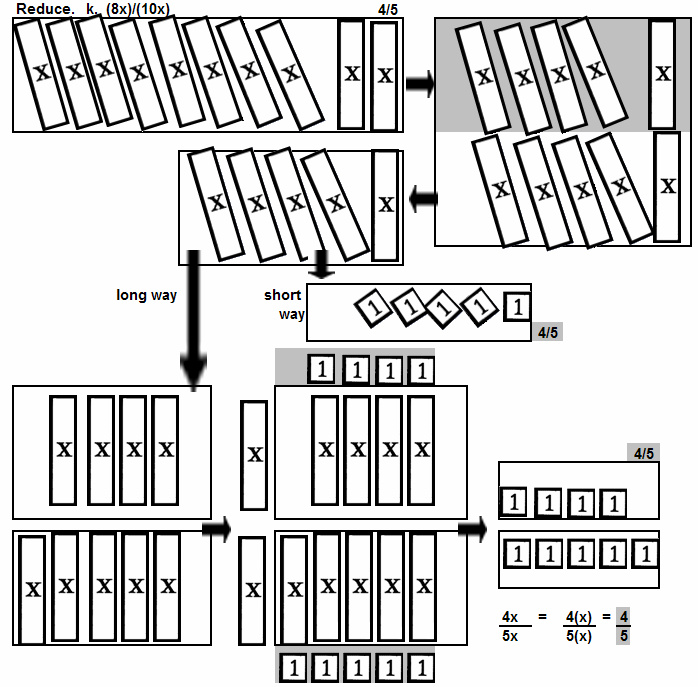
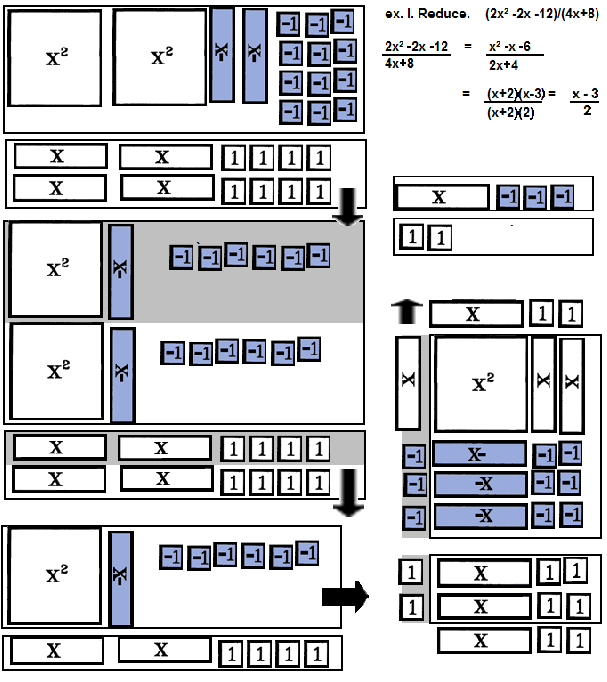
Reduce: j. 24/30, k. (8x)/(10x), l. (2x² -2x -12)/(4x+8)
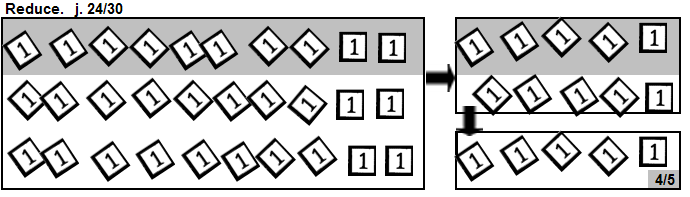
To reduce 24/30, creating 3 identical rows means there is a factor of 3 in the
denominator (because of the rows) and in the numerator (because of the identical). The fraction 24/30 may be
reduced to 8/10. To reduce 8/10, creating 2 identical rows means there is a factor of 2 in the denominator
(because of the rows) and in the numerator (because of the identical). The fraction 8/10 may be reduced to 4/5.
Reduce Fractions in Numerator / Denominator Form
| 1st: | Simplify the tiles in the numerator and
denominator display areas. |
| 2nd: | Factor the numerator, if possible. |
| 3rd: | Factor the denominator, if possible. |
| 4th: | Use the factors they DON'T have
in common as the new numerator and the new denominator.
Whenever possible, remove a top factor with an identical bottom factor.
TO REDUCE, USE THE
FACTORS
THEY DON'T HAVE IN COMMON
AS THE NEW NUMERATOR AND THE NEW DENOMINATOR.
|
|
| 5th: | Repeat steps 1 and 2 and 3 and 4 as often as needed. |
|








