[tutorials & resource material arranged by topic Class Table

How To Appreciate Logs Without Feeling Out On a Limb
           Log Laws and Experiments w/Log Computation


A LOG IS AN EXPONENT. A LOG IS AN EXPONENT.
restate
restate
restate
restate
restate
restate
restate The log of a sum can't be simplified unless the numbers are the same.
restate The log of a difference can't be simplified unless the numbers are the same.
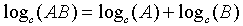restate When you multiply numbers, you add the logs.
restate When you divide numbers, you subtract the logs.
restate When you raise to a power, you multiply the logs.
restate When you take a root, you divide the logs.


Enter numbers as decimals, not fractions.
To Compute Using Logs:
  1. Choose a base.  c = 
     
  2. Take the logs of each number in this base.
    A = 
    B = 
     
  3. Add the logs to multiply.              
     
    Subtract the logs to divide.          
     
    Multiply the logs (the exponents) to raise A to the B power.    
     
     
    Divide the logs (the exponents) to take the Bth root of A .  

     
  4. Take the antilog of the result -- raise the base to this power.

      5.     (base)(sum)
          (base)(difference)

          (base)(product)
          (base)(quotient)
Vocabulary:
base
e
exponent
exponential function
log
logarithm
© 00-7-8, 10/21/2018, 2/25/2022, A2   www.mathnstuff.com/math/spoken/here/2class/340/loglaws.htm
[Applications] [Essays] Classes [Words] [Table] [Good Stuff] [MC,i. Home]