


Polynomials are expressions composed of terms.
Polynomials include binomials (expressions with two terms) and trinomial (expressions with three terms) and each of these are also considered polynomials (expressions with many terms). Some consider monomials (expressions with only 1 term) as polynomials though mono, one, does not mean poly, many.
To ADD polynomials which are like, one combines like terms -- factor and simplify or add the coefficients and copy the bases and their exponents.
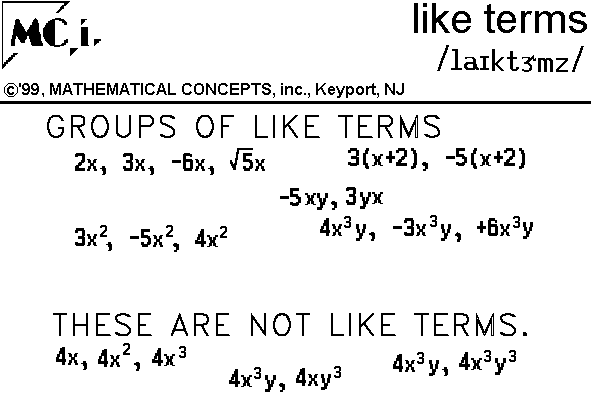
To SUBTRACT polynomials which are like, one distributes the negative and combines like terms. [So an expression like (4x - 2) - (3x + 1) becomes 4x -2 - 3x - 1, then x - 3.]
MULTIPLICATION of polynomials works like multiplication of constants -- each term of one factor polynomial is multiplied by each term of the other factor polynomial, then, like terms are combined.
| Multiply: 234(51) 234 x51 ----------- 234 1170 ------------ 11934 | Multiply: (2x2+3x+4)(5x+1) 2x2+3x+4 5x+1 --------------------- 2x2+3x+4 10x3+15x2+20x ----------------------------- 10x3+17x2+23x+4 |
To SQUARE means to use the expression to be squared as a factor twice, perform the multiplication, then combine like terms. [The expression (x+3)2 becomes (x+3)(x+3), becomes x2 +3x + 3x + 9, becomes x2 + 6x + 9.
To CUBE means to use the expression to be cubed as a factor three times, perform the multiplication, then combine like terms.
To "FOIL" means to multiply two binomials, multiplying FIRST terms, then OUTER terms, then INNER terms, then LAST terms. To repeat the amination below, press REFRESH or RELOAD on your browser..

DIVISION of polynomials works much like division of constants.

To "UNFOIL" means to reverse the multiplication by factoring. An animation of the factoring of 1x² + bx + c is provided here. Additional resources are listed below.
Resources
|

![[MC,i. Home]](http://www.mathnstuff.com/math/spoken/here/1gif/mcihome.gif)
![[Table]](http://www.mathnstuff.com/math/spoken/here/1gif/table.gif)
![[Words]](http://www.mathnstuff.com/math/spoken/here/1gif/words.gif)

![[this semester's schedule w/links]](http://www.mathnstuff.com/gif/semestr.gif)
![[Good Stuff -- free & valuable resources]](http://www.mathnstuff.com/gif/goods.gif)
|
www.mathnstuff.com/math/spoken/here/2class/220/c22pg00.htm |