IN MATH: 1. n. the
function, or rule which
produces the "greatest integer less than or equal to the number"
operated
upon, symbol [x] or sometimes [[x]].
The greatest integer function is a
piece-wise defined function.
- If the number is an
integer, use that integer.
- If the number is not an
integer, use the next smaller integer.
Examples:
number | the greatest integer less than or equal to the number
x | [x]
4 | [4] = 4
4.4 | [4.4] = 4
-2 | [-2] = -2
-2.3 | [-2.3] = -3
IN ENGLISH: 1. as defined above.
APPLICATIONS:
- 1. Complete given [x], the greatest integer less than or equal to a number.
- a.) [6.2]
- b.) [-6.2]
- 2. List an application, use, of this function.
-

This is a page from the dictionary
MATH SPOKEN HERE!, published in 1995 by MATHEMATICAL CONCEPTS, inc.,
ISBN: 0-9623593-5-1. You are hereby granted permission to make ONE printed copy of
this page and its picture(s) for your PERSONAL and not-for-profit use.

 Click on the [[x]] image for additional info.
Click on the [[x]] image for additional info. 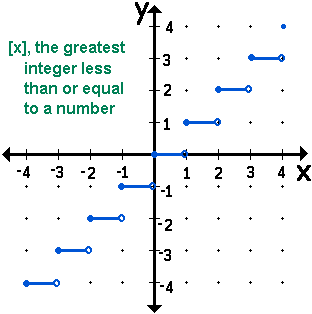


![[MC,i. Home]](http://www.mathnstuff.com/math/spoken/here/1gif/mcihome.gif)
![[Table]](http://www.mathnstuff.com/math/spoken/here/1gif/table.gif)
![[Words]](http://www.mathnstuff.com/math/spoken/here/1gif/words.gif)

![[this semester's schedule w/links]](http://www.mathnstuff.com/gif/semestr.gif)
![[Good Stuff -- free & valuable resources]](http://www.mathnstuff.com/gif/goods.gif)
![[next]](http://www.mathnstuff.com/math/spoken/here/1gif/next.gif)
![[last]](http://www.mathnstuff.com/math/spoken/here/1gif/last.gif)