Name ___________________________________________ © 2008, A. Azzolino   www.mathnstuff.com/papers/condots/prose.htm Oscar Reutersvard's Penrose Square -- Solve the quadratic. Connect the answers in order, perhaps w/a straightedge.

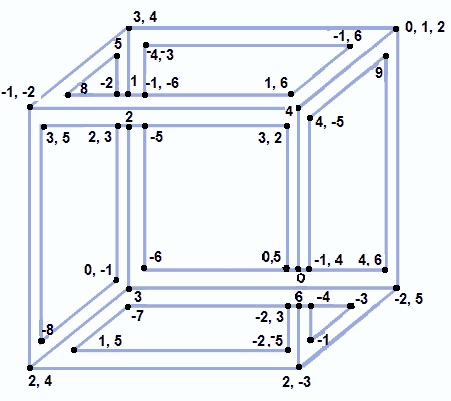
Start a new line. 1. x² - 8x + 16 = 0     {4} 2. (x + 1)(x + 2) = 0     {-1, -2} 3. x² - 7x +12 = 0     {3, 4} Start a new line. 4. x² + 3x = - 2     {-1, -2} 5. (x - 2)(x - 4) = 0     {2, 4} Start a new line. 6. x² + 1x - 6 = 0     {2, -3} 7. x² - 3x - 10 = 0     {-2, 5} 8. x² - 6x + 9 = 0     {3} 9. x² = 6x - 8     {2, 4} 10. x² + x = 6     {2, -3} 11. (x - 6)² = 0     {6} 12. x² + 5x + 9 = - x     {-3} 13. x² + 1 = - 2x     {-1} 14. x² + 8x + 16 = 0     {-4} 15. x² + 14x + 49 = 0     {-7} 16. x² - 6x + 5 = 0     {1, 5} 17. x² + 7x + 10 = 0     {-2, -5} 18. x² - x - 6 = 0     {-2, 3}

Start a new line. 19. x² - 3x - 4 = 0     {-1, 4} 20. x² + x - 20 = 0     {4, -5} 21. x² - 18x + 81 = 0     {9} 22. x² - 10x + 24 = 0     {4, 6} 23. x² + 12x + 36 = 0     {-6} 24. (x + 5)² = 0     {-5} 25. x² - 8x + 15 = 0     {3, 5} 26. x² + 16x + 64 = 0     {-8} 27. x(x + 1) = 0     {0, -1} 28. x² - 5x + 6 = 0     {2, 3} 29. x² - 4x + 4 = 0     {2} 30. x² - 6x + 9 = 0     {3} Start a new line. 31. x² + 10x + 25 = 0     {-5} 32. - x² + 5x - 6 = 0     {3, 2} 33. x² - 5x = 0     {0, 5} 34. x² = 0     {0} 35. x² - 8x + 16 = 0     {4} 36. x(x-1)(x-2) = 0     {0, 1, 2} 37. x² - 3x - 10 = 0     {-2, 5}

Start a new line. 38. x³ -3x² +2x = 0     {0,1,2} 39. 12 + x² = 7x     {3,4} 40. x² - 2x + 1 = 0     {1} 41. (x - 8)² = 0     {8} 42. x² - 10x + 5 = - 20     {5} 43. x² + 4x + 4 = 0     {-2} 44. x² - 7x + 6 = 0     {1, 6} 45. x² - 5x - 6 = 0     {-1, 6} 46. x² + 7x + 12 = 0     {-4, -3} 47. x² + 7x + 6 = 0     {-1,-6}