Change a Decimal to A Fraction
Rationals (Fractions) Read the number
without the word point. Write the fraction.
Irrationals (Nonfractions)
Approximate with a fraction.
Some decimal/fraction equivalents one should "just know."
Decimals/fraction equivalents like .5 is 1/2 or that .75 is 3/4 or that .3333... is 1/3
or that .12112111211112... does not have an equivalent fraction are examples of what one is expected to
know in most high school math classes. The procedures below may be used when these equivalents are not
recognized by sight.
Decimal numbers which repeat may be written as fractions -- they are
rational. Decimal numbers which do
not repeat can not be written as fractions -- they are
irrational numbers.
There are two kinds of repeating decimals: those which repeat from the
decimal point (with the tenths-place) and those which do not begin to repeat in the tenths-place.
Decimals like .5 and .25 look like they don't repeat, but, they do. They do not begin
to repeat until "after" the tenths-place.
The decimal .5 is also written as .50 or .500 or .5000 or .5000000..., the 0 is a
single repeating digit. So, though .5 does not look like an infinite repeater, it does have an infinite number of
decimal digits "on the right." The numbers .25, .168, 4.37905, and other decimal numbers which also look like
they do not repeat also have an infinite number of 0 decimal digits "on the right."
 Decimals Which "Do Not Repeat" (Have Repeating Zeros) - Decimals Which "Do Not Repeat" (Have Repeating Zeros) -
- 1st: Determine the name of the last decimal
place.
- (hundreds)(tens)(ones)
(tenths)(hundredths)(thousandths)(ten-thousandths)(hundred-thousandths)
- (100)(10)(1)(1/10)(1/100)(1/1000)(1/10,000)(1/100,000)
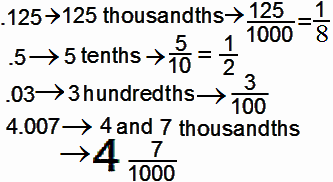
- 2nd: Create a fraction with the place from step 1.
- Use the place name as the denominator.
- 3rd: Remove the decimal from the expression and
- write the remaining number in the top (numerator) of the fraction.
- 4th: Write as a mixed number as needed.
- 5th: Reduce if possible.
 Decimals Which Repeat from the Decimal Point, In the Tenths-Place
Decimals Which Repeat from the Decimal Point, In the Tenths-Place
- 1st: Count the number of digits in the pattern which repeats.

- The number .3333... has 1 repeating digit.
- The number .575757... has 2 repeating digits.
- The number 4.127... has 3 repeating digits.
- 2nd: Use this number of 9s as digits in the denominator of the fraction.
- A one-digit repeater has one 9, /9, ninths.
- A two-digit repeater has two 9s, /99, ninety-ninths.
- A three-digit repeater has three 9s, /999, nine-hundred-ninety-ninths.
- 3rd: Use the repeating digit(s) as the numerator.
- 4th: Use the required number of 9s as the denominator.
- 5th: Write as a mixed number as needed.
- 6th: Reduce if possible.
 Decimals Which Repeat But Not from the Decimal Point, Not from the Tenths Place
Decimals Which Repeat But Not from the Decimal Point, Not from the Tenths Place
- 1st: Determine the name of the last decimal place that does not contain a repeating digit.
- (hundreds)(tens)(ones)
(tenths)(hundredths)(thousandths)(ten-thousandths)(hundred-thousandths)
- (100)(10)(1)(1/10)(1/100)(1/1000)(1/10,000)(1/100,000)
- 2nd: Create a fraction with the place from step 1.

- Use the place name as the denominator.
- 3rd: Move the decimal from the expression
- to the left of repeating digits and
- write the remaining number,
- INCLUDING THE REPEATING PART,
- in the top (numerator) of the fraction.
- 4th: Rewrite the repeating decimal
- from the numerator (top) of the fraction
- so that the numerator is a mixed number.
- See above.
- 5th: Multiply the ENTIRE fraction by 1
- in the form of
- (numerator's denominator)/(numerator's denominator).
- 6th: Complete the arithmetic.
- 7th: Reduce if possible.
|


 With Same Denominators --- add tops, keep bottom
With Same Denominators --- add tops, keep bottom
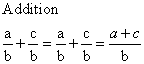


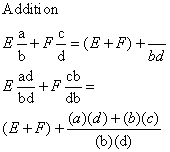
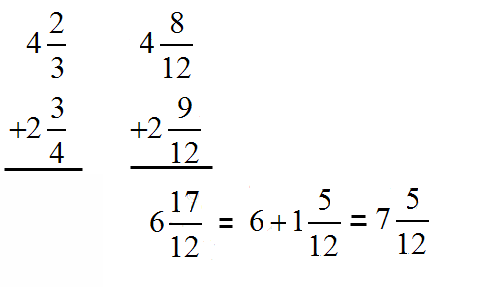

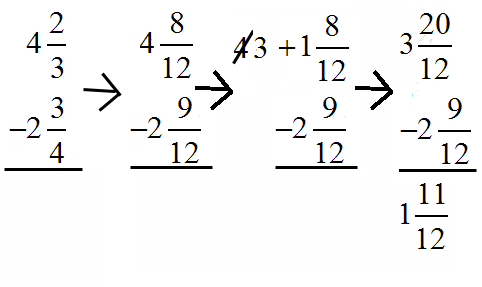

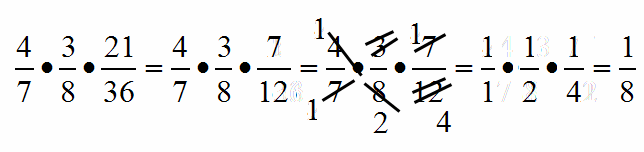

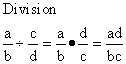
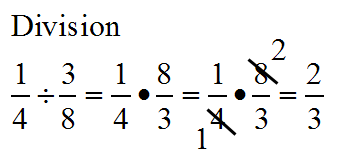
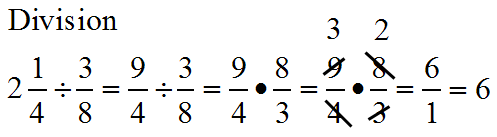






 PERCENT
PERCENT  PERCENT
PERCENT 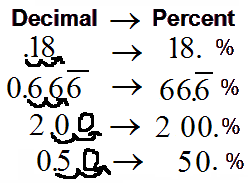
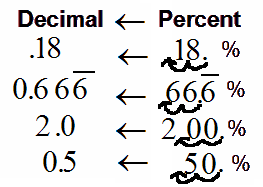
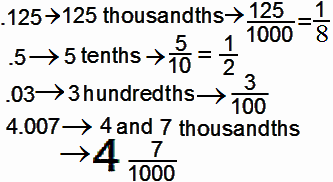



![[MC,i. Home]](http://www.mathnstuff.com/math/spoken/here/1gif/mcihome.gif)
![[Words]](http://www.mathnstuff.com/math/spoken/here/1gif/words.gif)

![[this semester's schedule w/links]](http://www.mathnstuff.com/gif/semestr.gif)
![[Good Stuff -- free & valuable resources]](http://www.mathnstuff.com/gif/goods.gif)