Ancient Egyptian
Multiplication,
Division,
Root Extraction
-- Computation

Contents Multiplication by Doubling and Halving (Mediation & Duplation) Multiplication Examples Decomposition into Powers of 2 How the Doubles Are Chosen Written Work Multiplication by Decomposition Division by Repeated Subtraction and by Sum of Identified "Doubles" Unit Fraction and Negative Powers of Two References

Ancient Egyptian Multiplication       In the 1850s, a Scottsman named A. H. Rhind purchased a papyrus of Egyptian mathematics and a leather roll. The papyrus is collection of completed math problems and is called the Rhind Papyrus or the Ahmes Papyrus. Ahmes was the scribe who in 1650 BCE copied the math from a much older document. The Egyptian Mathematical Leather Roll (EMLR) contains methods for simplifying a series (a sum) of unit fractions to a single unit fraction. Much of the Rhind Papyrus deals with fraction computation, area problems, and "solving equations" -- finding the value of a heap.       On this web page multiplication, division, and some fractions ancient Egyptian style are discussed.       The multiplication method is sometimes called doubling and halving or called Russian peasant multiplication. In modern terms it employs the decomposition of one number into its binary components, addition to produce "doubles" or multiples of the other number, and computing a total of doubles identified by odd divisors or the powers of two. Ancient Egyptians did not use this vocabulary and neither need you, but, the method will is examined below using a modern version of the algroithm and examples.

Multiplication by Doubling and Halving (Mediation & Duplation)       To multiply two numbers by doubling and halving: 1st: Place each number at the top of one of two side-by-side columns. One column's entries are doubled and the others are divided by two. To shorten the computation and format the problem as shown in these examples, put the smaller number at the top of the left column and use dividing to produce other entries in that column as directed below. 2nd: Create entries in the left column by halving the number in the row above it and discarding the remainder. Stop at 1 or 0. 3rd: Create entries in the right column by doubling the number in the row above it. Stop when you have matched all the rows of the left column. Note: Rather than double the number to obtain the next number, reference and internet sources use the phrase "add it to itself" to get the next number. 4th: Use the odd numbers in the left column to identify which matching numbers in the right column to add. 5th: Add the "doubles" in the right column which match the identified powers of two from the left column. 6th: The sum is the desired product.

Decomposition into Powers of 2       Earlier "the decomposition of one number into its binary components" and "the powers of two" were mentioned as important in the multiplication process. Consider now the powers of two.       The numbers 1, 2, 4, 8, 16, 32, 64, ... have been arranged in ascending and descending order and as simple constants and as powers. They are "colored" so one may easily track and follow the patterns below.       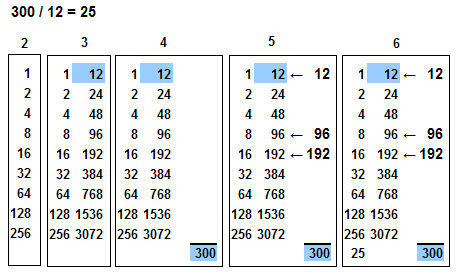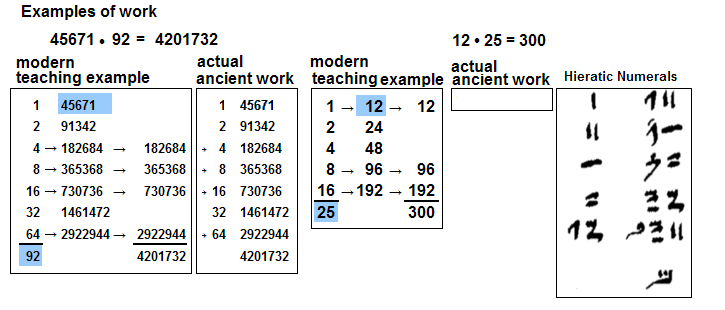Earlier the numbers 92, 25, and 15 were used as multipliers. For this reason they were chosen to help explain decomposition, ordered breaking-down, into the powers of 2.       Three different representations of 92, 25, and 15 are shown.       On the left, repeated subtraction of the largest possible power of 2 is presented.       On the right, the numbers are represented in modern binary notation and below that as the sum of the powers of two.       The sum of the powers of two is required in ancient Egyptian multiplication by havling and doubling.

How the Doubles Are Chosen - The Odd Halves Match the Powers of 2       Expressing a number as the sum of powers of two is important.       The idea of multiple is important. To multiply 10 by 3, find the 3rd multiple of 10. The multiples of 10 are 10, 20, 30, 40, … The 3rd multiple is 30. To multiply 3 by 10, find the 10th multiple of 3. The multiples of 3 are 3, 6, 9, 12, 15, 18, …, 27, 30, 33, … The 10th multiple of 3 is 30.       Because 92 may be expressed as the sum of powers of two, the product of 92 and 45671 may be expressed as the sum of the multiples of 45671 which match the required powers of two.

Written Work       The Rhind Papyrus was not written in more ancient hieroglyphics but in Hieratic notation. Just for fun, the 12 x 25 problem is shown on the left in Hieratic numerals. Hieratic is an additive system. The scribe didn't bother with check marks or the totals the teaching model displays. Can you read it?

Multiplication by Decomposition       To multiply two numbers using powers of 2: 1st: Use two side-by-side columns of numbers. The left column will contain the multiplier and powers of two. The right column will contain multiples of the multiplicand and the product. Additional columns of checks or marks and of identified "doubles" may be placed as desired by the scribe. 2nd: Begin at the top of the left column and fill the column in order with the powers of two until you have reached the multiplier. 3rd: If the multiplier is a power of two write this row twice. If the multiplier is not a power of two, write the multiplier only once at the bottom of the left column. 4th: On the top row of the right column place the multiplicand. 5th: Create the remaining entries in the right column by doubling the number in the row above it. Stop when you have matched all the rows of the left column except for the multiplier. 6th: Check or mark the powers of two required to decompose the multiplier.       In the example above the multiplier is 25. The numbers 16, 8, and 1 are identified because 25 = 16 + 8 + 1, the decomposition of 25. 7th: Add the "doubles" in the right column which match the identified powers of two from the left column. The scribe may create a new column or use the existing right column. 8th: The sum is the desired product.

Division       Yes, division may be completed by repeated subtraction. The following algorithm will also complete division. It may be difficult to find the sum of "doubles."       To divide: 1st: Use two side-by-side columns of numbers. The left column will contain powers of two (and eventually the quotient). The right column will contain multiples of the divisor. Additional columns of checks or marks and of identified "doubles" may be placed as desired by the scribe. 2nd: Begin at the top of the left column and fill the column in order with the powers of two until you have reached the dividend. 3rd: On the top row of the right column place the divisor. 4th: Create the remaining entries in the right column by doubling the number in the row above it. Stop when the "double" is as large as the dividend. 5th: This is the tough task. Find and check or mark "doubles" in the right column so that their sum is the dividend. 6th: The sum of the indicated left-column powers of two is the quotient.

Unit Fractions and Negative Powers of Two       The Egyptians used unit fractions long before calculus teachers taught students Taylor and McLauren and other power series.       They use a third and a fifth and any other unit fraction needed and symbolized it by an open mouth written above the number. The most important fractions were those above. The most famous idea was the one below.

References Azzolino, Agnes. "multiple" © 2005 at www.mathnstuff.com/math/spoken/here/1words/m/m29.htm visited 10 April 2009. Betṛ , Maria Carmela. "THE EYE OF HORUS" at http://www.amun.com/eng/horus_e.html visited 12 August 2009 Gardner, Milo. "Egyptian Mathematical Leather Roll." © 1999-2009 Wolfram Research, Inc. at http://mathworld.wolfram.com/EgyptianMathematicalLeatherRoll.html visited 12 August 2009. Gnaedinger, Franz "Rhind Mathematical Papyrus" © 1979 - 2003 visited 12 August 2009. Newman, James Roy.   The World of Mathematics through a Google books search for "text of the rhind papyrus" at http://books.google.com visited 10 August 2009. O'Connor, J J & Robertson, E F. "Egyptian Mathematics" © 2006 at http://www.math.utep.edu/Faculty/lvaliente/Math1319/Egyptian.doc visited 9 August 2009 Smith, Jr., Frank D. (Tony) "Hieroglyphics: Egyptian, Mayan, and Chinese Characters" at http://www.valdostamuseum.org/hamsmith/eghier.html visited 11 August 2009. Stone Design Corp. "The Eye of Horus " at http://www.stone.com/Qouija/Eye_of_Horus.html visited 11 August 2009. Wikipedia, the free encyclopedia "Eye of Horus" at http://simple.wikipedia.org/wiki/Eye_of_Horus visited 11 August 2009.

© 2009, Agnes Azzolino www.mathnstuff.com/math/spoken/here/2class/60/egyptm.htm