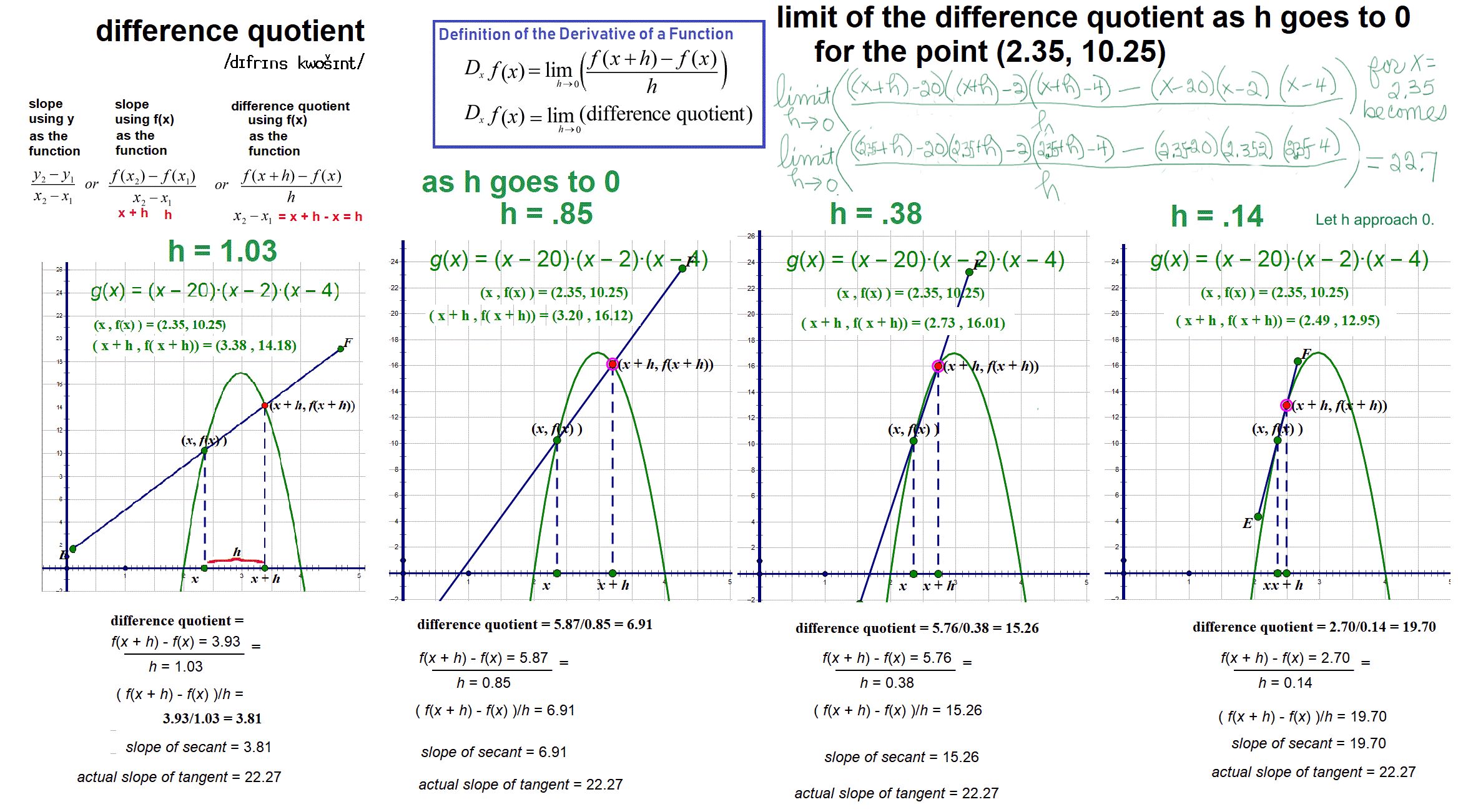
Before one can take a derivative by taking the limit of a difference quotient, one needs to know what a difference quotient and a limit are.

      Difference is a subtract expression, as in the difference between two numbers, as in the difference between 9 and 7 is 9 - 7 or 2. The difference may be between a function at one value of x and the function of another value of x is f(x₂) - f(x₁). To find a difference, just subtract.

      Quotient is a division expression, as in the result when two numbers are divided, as in the quotient 8 ÷ 2 is 4. To find a quotient, divide. Remember also that a division expression may be written as a fraction, as in, numerator / denominator,
      12/7, or
      (4 -1) / (-9-3), or
      [f(x₂) - f(x₁)]/[x₂ - x₁].

      A difference quotient is a fraction (a division expression) in which the numerator is a difference in function values and the denominator is a difference in x values -- JUST LIKE SLOPE!

      To take a limit, think "approach." Use the sketchpad in the box to examine "approach."

Use Dynamic Analytic Geometry to Take A Limit

      Click to enlarge or isolate an image.

        Derivative Proofs    
        d(e^x)/dx= e^x
        d( sin(x) )/dx = cos(x)  
        more examples