More Trig Equations to Solve
Other Resource PagesSolving Equations Graphically, Solutions to Linear Equations

compute.xls -- Spreadsheet which solves linear and quadratic equations and linear systems

Precalc Notes -- Links to an entire precalc course material

solvtrg.xls -- Spreadsheet which solves triangles by different methods


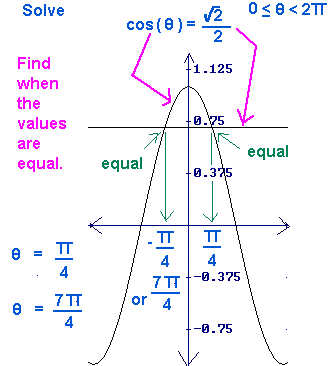
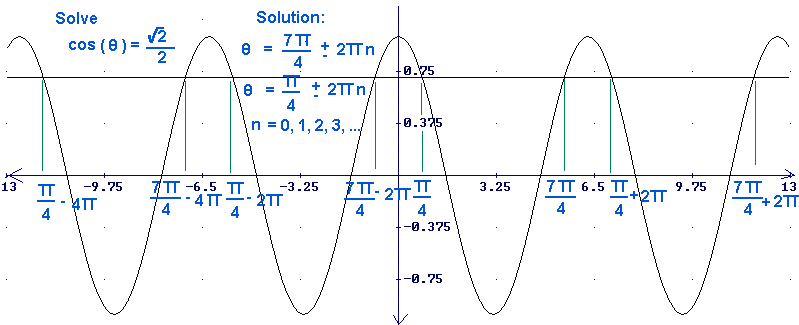
 ) =
) =
 <
<






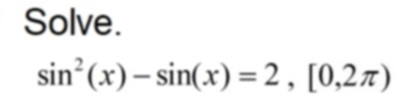







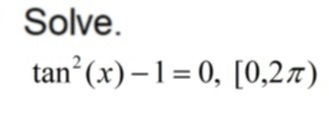



![[MC,i. Home, site home page]](http://www.mathnstuff.com/math/spoken/here/1gif/mcihome.gif)
![[master list of all MSH! dictionary words]](http://www.mathnstuff.com/math/spoken/here/1gif/words.gif)

![[Good Stuff -- free & valuable resources]](http://www.mathnstuff.com/gif/goods.gif)
![[this semester's schedule w/links]](http://www.mathnstuff.com/gif/semestr.gif)