Area is the number of square units. In arithmetic, the numbers used to compute areas are constants.

    In algebra, the numbers used to compute area are often variables or variable expressions, linear expressions, like one more than a number, x+1, or double an number, 2x.

    In algebra, (line)(line) = (quadratic) so the quadratic is important in expressing area.

    The perimeter of a rectangle is 24 cm. Find the maximum area of the rectangle.

    The solution is an area of 36 square units achieved using a rectangle which is a square, in this case, a 6 unit by 6 unit rectangle.

    For a given perimeter, the square ALWAYS yields the MAXIMUM AREA.

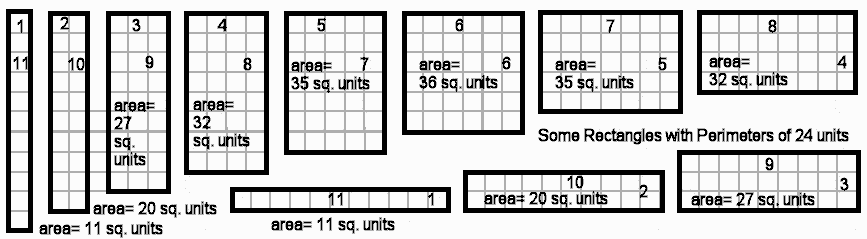
    We will examine the reason from 3 points of view -- arithmetic, algebra II, calc.

    The perimeter of a rectangle is 24 cm. Find the maximum area of the rectangle.

    The 6 by 6 square yields the solution, an area of 36 square units

    For a given perimeter, the square ALWAYS yields the MAXIMUM AREA.

    In arithmetic, one doesn't prove that a square has the maximal area.

    In arithmetic, one examines the possible rectangles and uses guess-and-test to see if the best answer can be found.

    You are invited to use the web page to try to maximize area for a given perimeter.

    The perimeter of a rectangle is 24 cm. Find the maximum area of the rectangle.

    The 6 by 6 square yields the solution, an area of 36 square units

    In algebra II, the y-value of the vertex of the parabola ALWAYS yields the MAXIMUM or MINIMUM value depending on the concavity of the parabola.

    The area of a rectangle is (base)(height). Use x for the base and the fact that the perimeter is 24 units. The area becomes (x)(12-x) or -x² +12x.

    If you've studied the pages on composition of functions and dilation, note that this vertex happens when the two factors are equal -- when (x) equals (12-x), the solution of x=12-x, the value 6.

    If you've studied the use of the calculator, you will appreciate that in the CALC menu, the maximize function produces the best results it can. It states the side as 5.9999994 but states the accurate area of 36 as the maximum value of the function.

    The perimeter of a rectangle is 24 cm. Find the maximum area of the rectangle.

    The 6 by 6 square yields the solution, an area of 36 square units

    In calc, the function evaluated at the solution obtained when the derivative is set equal to zero ALWAYS yields the RELATIVE MAXIMUM or MINIMUM or the MAXIMUM or MINIMUM value of the function if one exists.

    Take the area formula: (x)(12-x) or -x² +12x. Take its derivative: -2x + 12. Set the derviative equal to 0. Solve. Use this x value to evaluate the function. That yields the maximum area.

Take the area formula: (x)(12-x) or -x² +12x.

 

Take its derivative: -2x + 12.

 

Set the derviative equal to 0: -2x + 12 = 0

 

Solve:

-2x + 12 = 0

-2x = -12

-2x/(-2) = -12/(-2)

x = 6

 

Use this x value to evaluate the function.

If f(x)= (x)(12 - x), then f(6) = (6)(12-6) = (6)(6) = 36

 

That is the maximum area.

    A rectangular pasture is bordered on one side by a stream. On the other 3 sides are fenced in by 1500 m of fencing. Find the dimensions of the pasture that maximizes the area enclosed.

    The area of this rectangular field is
(height)(base) is
(x)(1500-2x).

    The graph, table of values, and solver solutions generated by calculator, yield the maximum area of 281250 m² using a height of 375 m and therefore a base of 750 m. Note that the maximum area is achieved using two 375 m by 375 m squares.