[tutorials & resource material arranged by topic Class Table

RADICAL IDEAS, Rational & Irrational Numbers and Roots




Rational & Irrational, but Not the Other Complex Numbers
 

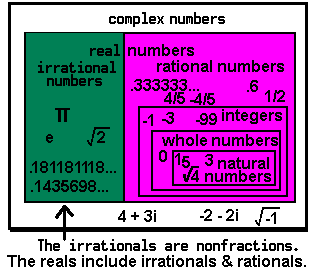
    This page deals with the two kinds of real numbers, the rationals (or fractions) and the irrational numbers (or nonfractions).   It deals with the pink and green numbers on the left.

    This page does not deal with those complex numbers (see imaginary numbers) which are not real.   It does not deal with the white numbers on the left.

    One often uses the rationals and irrationals when working with the Pythagorean Theorem, the quadratic formula, and with the quadratic equation and discriminant.   Most often irrationals are used when taking a square root.

 
 
 
 
Vocabulary
 

    The radical expression at the left, the square root of 25, has an index of 2 and a radicand of radicand of 25.   The "square root of 25" means the "number whose square is 25."   The radical sign includes both the v-shaped mark at the left and the horizontal inclusion bar.

    Mathematicians have made an agreement. Because the index is even (2, 4, 6, ...) and there are two possible roots, mathematicians have agreed to use the positive or principal root, 5, to simplify the expression.   So, even though -5 also fits the description the "numbers whose square is 25," only the 5 is used as the principal root.

 
 
 
 
Simplify vs. Solve
 
Simplify: 25   vs.   Solve: x2 = 25
Simplify: x2   vs.   Solve: x2 = a

    The difference between simplify, make less complex, and solve, find all possible answers, and the idea of equation vs. expression are crutial understanding why the square root of 25 is 5 and the x in x2 = 25 is 5 or -5.   These understood, it's easy.

    The square root of 25 is 5 becasue though both 5 and -5 work, mathematicians agree to use the positive, simpler, root. The x in x2 = 25 is 5 or -5 because both numbers solve the equation, both make the equation true.

    x2 is |x| because, the absolute value guarentees the number is positive, yielding the simpler principle root.   The roots to x2 = a are +a and -a (which shorten to ± a) because each number makes the equation true.

 
 
Compute
 

    For computation with IRRATIONAL numbers see Radicals.

    For computation with RATIONAL numbers see Fractions.

Class Table [MC,i. Home] [Table] [Words] Classes [this semester's schedule w/links] [Good Stuff -- free & valuable resources]
© 2005, Agnes Azzolino
www.mathnstuff.com/math/spoken/here/2class/270/c27pg00.htm