To prove, by paper folding, the area of a circle is stated in the formula A = r².

• a set of PREVIOUSLY MADE circluar papers for instructor use

• descriptions and vocabulary for the circle
• definition of area,
• area formula for a parallelogram.

      Review at least as much about area as is discussed in rectangle.

      Review circle vocabulary, area, area of a rectangle, area of a parallelogram.

 

      The rectangle and the parallelogram must be done before the circle.

 

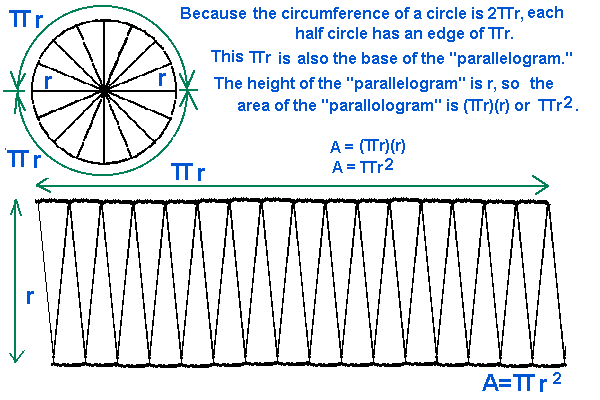
      The illustration above shows in symbols and graphically that a circle cut in pie-shaped pieces and rearranged, may be treated as a parallelogram for purposes of computing its area.

 

      To graphically see this transformation, look at in sequence, the circle divided in half, then in quarters, then in eighths, then in sixteenths, then in thirty-secondths.

 

      If this process were to continue, cutting the area into smaller pie-shaped pieces, each piece would still have the same height, the original radius of the circle, and though each curved edge would become smaller in length, the curved edges placed on the base would be half of the curved edges of the circle, r.

 

      Stated again in slightly different words: Since the circumference of a circle of radius r is 2 r, each half-circle has a perimeter or curved length of r.

 

      The radius r, and half the circumference, r, are the height and length of a "parallelogram." Since the area a parallelogram is (base)x(height) the area of the circle is ( r)x(r) or r².

 

      Stated again just in symbols:

A= bh

A= r(r)

A=r²

 

      HERE is a large circle marked to be divided into 64ths. It is left to the reader to make the whole, halved, quartered, eighthed, sixteenthed, 32thed, and 64thed copies of this image then to cut, rearrange, and tape the pieces together to make the set of manipulatives which show the transformation from a circle of unknown area to a "parallelogram" in which the area may be computed to be r². It is worth the time to create the set needed for the transformation. The manipulatives provide a powerful and simple way to explain a complex fact.

 

 

© March 3, 2003

www.mathnstuff.com/math/spoken/here/2class/150/areac.htm