|
Example 3a.
in the Warm Ups, from the last page and just below, is a SYSTEM of linear equations presented as a SINGLE
sophisticated linear equation. To solve it, substitution is employed. Below, examine it now from a linear
system perspective.
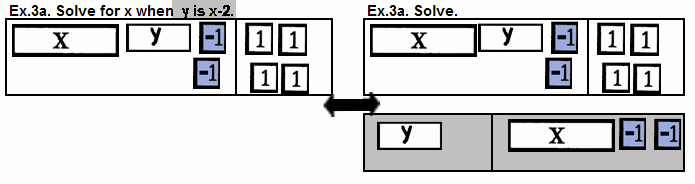 Solve Linear Systems by Substitution.
Solve Linear Systems by Substitution.
| 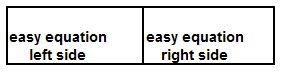 |
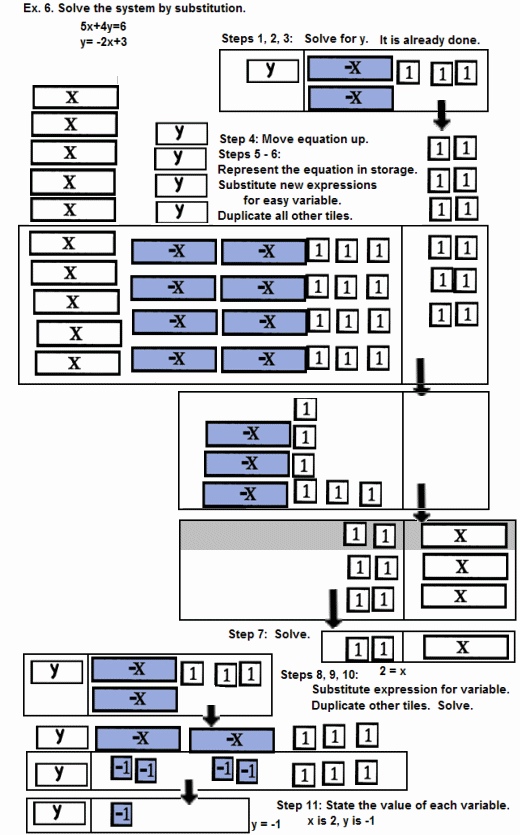
| 1st: | Use two display areas side-by-side for representing
an equation. (These will later be moved to the top away from the user.) |
| 2nd: | Pick one equation to solve for one variable. Take the
easy equation and the easy variable or use another method. |
| 3rd: | Solve the equation for the variable of choice. |
| 4th: | Move the solved equation in the side-by-side display
areas to the top, away from the user, and use two additional side-by-side display areas for the other
equation, placing them on the bottom close to the user. |
|
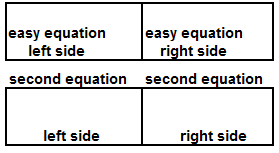 |
| 5th: | Represent the other equation IN THE STORAGE AREAS
ABOVE THE DISPLAY AREAS. |
| 6th: | In the bottom display areas,
SUBSTITUTE, replace, each of the solved variable tiles with the expression found in the third step and
duplicate exactly all other tiles. |
| 7th: | Solve the equation from the step six. |
| 8th: | Move the easy equation to the top storage areas above
the display areas. |
|
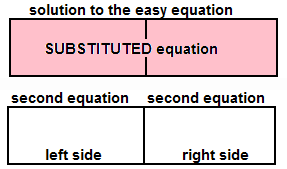 |
| 9th: | In the top display areas,
SUBSTITUTE, replace, each of the other variable tiles with the new value from step 7 and duplicate exactly
all other tiles. |
| 10th: | Solve the easy equation. |
| 11th: | State the solution and include values for both
variables. |
|


 Solve Linear Systems by Substitution.
Solve Linear Systems by Substitution.



