|
To divide two fractions: Copy the first fraction. Invert and multiply the second
fraction.
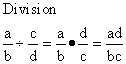
If you need to know why, see
"Remind Me Why "Invert and Multiply" Works When Dividing Fractions.".
Each Term Tile method used to divide fractions begins with representing the first
fraction and GOING DIRECTLY to inverting and representing the second fraction.
Division requires one to "flip"
the second
fraction then multiply.
 |

|
Tilted Tile Format is used only if all terms are of the same dimension or power --
all constant terms or all linear terms or all quadratic terms, for example. Tilted Tile Format may not be used if
any binomial is a part of the fraction.
It is best used to explain multiplication and division of fractions and this is
done in 4th, 5th, and 6th grades with constants.
Division of Proper Fractions in Tilted Tile Format
| Start: | More than one display area is required. |
| 1st: | Represent the first fraction in storage horizontally
on the top in the following way.
Let the denominator give you the number of tiles to be
used in each display area.
The denominator names the size.
Let the numerator give you the number of tiles to tilt at an angle to the edge.
The numerator names the number of fractional pieces. |
| 2nd: | Represent the second fraction in storage vertically
on the right in the following way.
This SWITCH of NUMERATOR and DENOMINATOR serves to INVERTS the fraction.
Let the NUMERATOR give you the number of tiles to be used in each display area.
Additional display areas may be needed. See multiplication for a similar
situation.
Let the DENOMINATOR give you the number of tiles to tilt at an angle to the edge. |
| 3rd: | Multiply. Fill the display area matching top tile to side tile in the
following way.
TILT ONLY the tiles which are TILTED on the top AND
ALSO TITLED on the side. |
| 4th: | Count all of the tilted tiles in all of the display area(s).
This is the numerator of the product. |
| 5th: | Count the number of tiles in any one of the display
areas. This is the denominator of the quotient. |
Division by an Improper Fraction by Tilted Tile Format
| Start: | More than one display area is required.
Each whole number and fraction (or mixed number) requires an edge -- its own area.
The final display areas must form a rectangle. |
| 1st: | Represent the first factor in storage horizontally on
the top in the following way.
Let the denominator give you the number of tiles to be used in
each display area.
The denominator names the size.
Let the numberator give you the number of tiles to tilt at an angle to the edge.
The numerator names the number of fractional pieces. |
| 2nd: | Represent the second factor in storage vertically on
the right in the following way.
Let the denominator give you the number of tiles to be used in each
display area.
The denominator names the size.
Let the numerator give you the number of tiles to tilt at an angle to the edge.
The numerator names the number of fractional pieces. |
| 3rd: | Multiply. Fill the display area matching top tile to side tile in the
following way.
TILT ONLY the tiles which are TILTED on the top AND
ALSO TITLED on the side. |
| 4th: | Count all of the tilted tiles in all of the
display area(s). This is the numerator of the product. |
| 5th: | Count the number of tiles in any one of the display
areas. This is the denominator of the quotient. |


| In Tilted Numerator / Denominator Format
| |
Divide Two Fractions in Numerator / Denominator Format
In Numerator / Denominator Format, the tile work for division BEGINS with
the multiplication by the inverse. Don't bother representing the division problem. Go directly to
representing multiplication by the inverse.
Divide Two Fractions in Numerator / Denominator Format
| 1st: | Use two display areas for each fraction.
Let the ones on the tops (further from the user) be for the numerators.
Let the ones on the bottoms (closer to the user) be for the denominators. |
| 2nd: | Represent the numerators in tops or uppermost
display areas. |
| 3rd: | Represent the first fraction in the first top and bottom
display areas. |
| 4th: | Invert, "flip," the second fraction. Represent the
2nd top in the bottom and the 2nd bottom in the top display area. |
| 5th: | Factor each numerator and denominator,
if possible. |
| 6th: | Use the factors they
DON'T have in common as the new numerator and the new denominator.
Whenever possible, remove a top factor with an identical bottom factor.
TO REDUCE, USE
THE
FACTORS THEY DON'T HAVE IN COMMON
AS THE NEW NUMERATOR AND THE NEW
DENOMINATOR. |
|
| 7th: | The product of the numerators is the numerator of
the product, the answer. |
| 8th: | The product of the denominators is the denominator
of the product, the answer. |
On the last page, "Multiplication of Fractions," most of the following division
problem was completed.
In the division problem stated, the next step is to invert the second
fraction and multiply is shown on the previous page. See
above and
example 4.




| 









