Correct use of the vocabulary words perimeter and area is more difficult for many beginning algebra student than is the computing of basic perimeters and areas.

      It is the teacher's job to judge how and when to use the more formal "mathematics vocabulary" or the less formal "math words."

      Here "Find the area of the circle" means "Find the area of the region enclosed by the circle" and the same terminology is used with rectangles, triangles, or other regions. Less formal expressions are used rather than the more formal to facilitate communication, but, it is the teacher's decision which to use. Definitions and an illustration of perimeter and area follow.

Perimeter

- measure of the length of the edge.

- the sum of lengths of the sides of a plane figure.

- the length of the border encircling a place or region.

            It is measured by length, one dimension.

            The perimeter is like the length of black string needed to trim the word area, below.

Area

- the measure of the size of the region enclosed by a plane figure.

- the number of square units enclosed by a plane figure. Area is a 2 dimensional measure.

The area is the number of FULL or PARTIAL square regions in the interior of each letter below.

      Area is easier to see than perimeter. Area is the number of squares in a region.

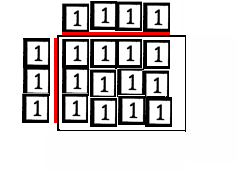
    Using 1-tiles, represent a rectangle in a display area.

[Below a 4 by 3 rectangle is represented. Others answers are likely.]

     

    Represent the width and length in top and side storage areas.

    Note on the times table, seen above on the right, that 12 is 3x4, (width)x(length).

This will work for any rectangle and a 30x50 table is available to examine this at prime.xls.

      Perimeter is more difficult to see than area because it is the length of the edge.

      Continue now with the tasks and example from above.

    Use the dimensions to compute the perimeter.

 

      The length of two edges, sides, of the rectangle is the

            (width)+(length), half the perimeter.

 

      [Below the red perimeter is 3+4 or 7 units

            and the blue piece is 3 + 4 or 7 units.]

 

    The length of all four edges, sides, is the perimeter.

 

      The perimeter is (width)+(length)+(width)+(length).

      Yes, the perimeter is also 2[(width)+(length)].

 

      [Below, the perimeter is 3+4+3+4 or 14 units.]