Storing tiles in sorted piles is suggested for the following reasons.

• In algebra, answers are usually written in descending order. Sorting tiles in descending order parallels this practice if tiles are ordered from left to right.
   
• Grouping tiles of the same type emphasizes that they represent different kinds of terms. Constants are not linear or quadratic or cubic terms. This means the constants, the x terms, the x² terms, and the x³ terms are different even though one might have the same number of each.
   
• Creating piles of many tiles visually differentiates them from the displayed tiles of a phrase, equation, or answer which requires individual tiles of pairs of zeros.

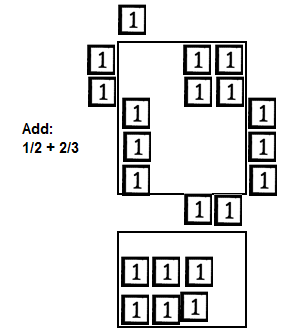
      For addition and subtraction, a display area created by an additional sheet of paper is suggested. For multiplication, division, and factoring it is even more important. For solving equations and inequalities and addition or subtraction of fractions, two display areas are required.

      There are a variety of ways to manipulate the tiles and a variety of situations in which movement is required.

      Writing expressions or equations is the most mentally taxing operation. Simplifying expressions and solving equations or inequalities are not nearly as difficult. WHEN WRITING OR REPRESENTING EXPRESSIONS OR EQUATIONS PERMIT THE MOST FLEXIBILITY.

      Once the expressions is represented, SIMPLIFY THE EXPRESSION FROM LEFT TO RIGHT to foreshadow the way in which written expressions are simplified.

      This left-to-right manipulation might be discussed with a class or simply modeled by the teacher as the teacher discusses the math that is being performed on the tiles.

      SOLVE AN EQUATION WITH TWO HANDS OR FROM LEFT-TO-RIGHT WITH ONE HAND. This will be discussed in greater detail when solving equations is discussed.